
【题目】某校在一次比赛中将所有参赛同学分为四个组,其中第一组有x人,第二组比第一组的![]() 少5人,第三组比第一、二组的和少15人,第一组的2倍与第四组的和是30人.
少5人,第三组比第一、二组的和少15人,第一组的2倍与第四组的和是30人.
(1)用含x的式子分别表示第二、三、四组的人数及参赛总人数;
(2)当x=10时,第四组与第三组相比,哪组的人数多?多多少人?
(3)x能否等于13,为什么?x能否等于20,为什么?
【答案】(1)第二组的人数:(![]() x﹣5)人;第三组的人数:(
x﹣5)人;第三组的人数:(![]() x﹣20)人;第四组的人数:(30﹣2x)人;参赛总人数:(3x+5)人:(2)第四组的人数多,多5人;(3)x不能等于13,见解析;x不能等于20,见解析
x﹣20)人;第四组的人数:(30﹣2x)人;参赛总人数:(3x+5)人:(2)第四组的人数多,多5人;(3)x不能等于13,见解析;x不能等于20,见解析
【解析】
(1)根据题意可用含x的代数式表示第二、三、四组的人数;
(2)把x=10代入计算可求第二、三、四组的人数;
(3)分别把x=13,x=20代入计算,根据整数的性质即可求解.
解:(1)第二组的人数:![]() 人;
人;
第三组的人数:![]() 人;
人;
第四组的人数:(30﹣2x)人;
参赛总人数:![]() ;
;
(2)当x=10时,
第三组的人数:![]() ;
;
第四组的人数:30﹣2x=30﹣20=10;
10﹣5=5(人).
故第四组的人数多,多5人;
(3)当x=13时,![]() ,
,
∵![]() 不是整数,
不是整数,
∴x不能等于13;
当x=20时,![]() ,
,
∵﹣10是负数,
∴x不能等于20.


 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案科目:初中数学 来源: 题型:
【题目】如图,已知矩形ABCD的周长为44cm,E是AD上的一点,F是AB上的一点,EF⊥EC,且EF=EC.

(1)若AF=6cm,求FC的长.
(2)连接BE,求证:BE平分∠ABC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下面三行数,
①2,-4,8,-16,32,-64……
②3,-3,9,-15,33,-63……
③-1,2,-4,8,-16,32……
取每一行的第![]() 个数,依次记为
个数,依次记为![]() ,如上图中,当
,如上图中,当![]() 时,
时,![]() ,
,![]() ,
,![]() 已知
已知![]() 这三个数中最大的数与最小的数的差为769,则
这三个数中最大的数与最小的数的差为769,则![]() 的值为__________.
的值为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将一条数轴在原点O和点B处各折一下,得到一条“折线数轴”.图中点A表示﹣10,点B表示10,点C表示18,我们称点A和点C在数轴上相距28个长度单位.动点P从点A出发,以2单位/秒的速度沿着“折线数轴”的正方向运动,从点O运动到点B期间速度变为原来的一半,之后立刻恢复原速;同时,动点Q从点C出发,以1单位/秒的速度沿着数轴的负方向运动,从点B运动到点O期间速度变为原来的两倍,之后也立刻恢复原速.设运动的时间为t秒.问:
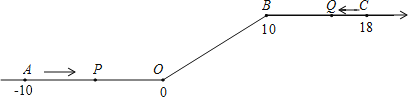
(1)动点P从点A运动至C点需要多少时间?
(2)P、Q两点相遇时,求出相遇点M所对应的数是多少;
(3)求当t为何值时,P、O两点在数轴上相距的长度与Q、B两点在数轴上相距的长度相等.
查看答案和解析>>
科目:初中数学 来源: 题型:
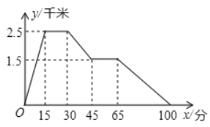
【题目】如图反映的是小华从家里跑步去体育馆,在那里锻炼了一阵后又走到文具店去买笔,然后走回家,其中x表示时间,y表示小华离家的距离.根据图像回答下列问题:
(1)小华在体育馆锻炼了_____分钟;
(2)体育馆离文具店______千米;
(3)小华从家跑步到体育馆,从文具店散步回家的速度分别是多少千米/分钟?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是某同学对多项式(x2-4x+2)(x2-4x+6)+4进行因式分解的过程.
解:设x2-4x=y
原式=(y+2)(y+6)+4 (第一步)
= y2+8y+16 (第二步)
=(y+4)2 (第三步)
=(x2-4x+4)2 (第四步)
回答下列问题:
(1)该同学第二步到第三步运用了因式分解的_______.
A.提取公因式 B.平方差公式 C.两数和的完全平方公式 D.两数差的完全平方公式
(2)该同学因式分解的结果是否彻底?________.(填“彻底”或“不彻底”)
若不彻底,请直接写出因式分解的最后结果_________.
(3)请你模仿以上方法尝试对多项式(x2-2x)(x2-2x+2)+1进行因式分解.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某汽车专卖店销售甲,乙两种型号的新能源汽车,上周售出甲型汽车和乙型汽车各2辆,销售额为88万元;本周售出3辆甲型汽车和1辆乙型汽车,两周的销售额为184万元.
(1)求每辆甲型汽车和乙型汽车的售价;
(2)某公司拟向该店购买甲,乙两种型号的新能源汽车共6辆,购车费不少于130万元,且不超过140万元.则有哪几种购车方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题再现:
数形结合是一种重要的数学思想方法,借助这种思想方法可将抽象的数学知识变得直观并且具有可操作性.初中数学里的一些代数公式,很多都可以通过表示几何图形面积的方法进行直观推导和解释.
例如:利用图形的几何意义验证完全平方公式.
将一个边长为![]() 的正方形的边长增加
的正方形的边长增加![]() ,形成两个长方形和两个正方形,如图所示:这个图形的面积可以表示成:
,形成两个长方形和两个正方形,如图所示:这个图形的面积可以表示成:
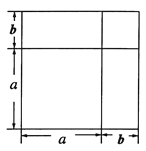
![]() 或
或![]()
∴![]()
这就验证了两数和的完全平方公式.
类比解决:
请你类比上述方法,利用图形的几何意义验证平方差公式.
(要求画出图形并写出推理过程)
问题提出:如何利用图形几何意义的方法证明![]() ?
?
如图所示,![]() 表示1个1×1的正方形,即:
表示1个1×1的正方形,即:![]() ,
,![]() 表示1个2×2的正方形,
表示1个2×2的正方形,![]() 与
与![]() 恰好可以拼成1个2×2的正方形,因此:
恰好可以拼成1个2×2的正方形,因此:![]() 、
、![]() 、
、![]() 就可以表示2个2×2的正方形,即:
就可以表示2个2×2的正方形,即:![]() 而
而![]() 、
、![]() 、
、![]() 、
、![]() 恰好可以拼成一个
恰好可以拼成一个![]() 的大正方形.
的大正方形.
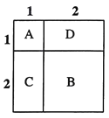
由此可得:![]() .
.
尝试解决:
请你类比上述推导过程,利用图形的几何意义确定:![]() _______.(要求写出结论并构造图形写出推证过程).
_______.(要求写出结论并构造图形写出推证过程).
问题拓广:
请用上面的表示几何图形面积的方法探究:![]() _______.(直接写出结论即可,不必写出解题过程).
_______.(直接写出结论即可,不必写出解题过程).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com