
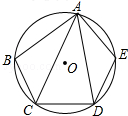
 如图,在圆的内接五边形ABCDE中,∠B+∠E=220°,则∠CAD=40°.
如图,在圆的内接五边形ABCDE中,∠B+∠E=220°,则∠CAD=40°.  科学实验活动册系列答案
科学实验活动册系列答案科目:初中数学 来源: 题型:解答题
| 鱼的条数/条 | 平均每条鱼的质量/kg | |
| 第1次捕捞 | 10 | 1.7 |
| 第2次捕捞 | 25 | 1.8 |
| 第3次捕捞 | 15 | 2.0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
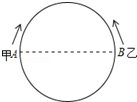 如图所示,甲、乙两点分别从直径的两端点A、B以顺时针、逆时针的方向同时沿圆周运动,甲运动的路程l(cm)与时间t(s)满足关系:l=$\frac{1}{2}{t^2}+\frac{3}{2}$t(t≥0),乙以4cm/s的速度匀速运动,半圆的长度为21cm.
如图所示,甲、乙两点分别从直径的两端点A、B以顺时针、逆时针的方向同时沿圆周运动,甲运动的路程l(cm)与时间t(s)满足关系:l=$\frac{1}{2}{t^2}+\frac{3}{2}$t(t≥0),乙以4cm/s的速度匀速运动,半圆的长度为21cm.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
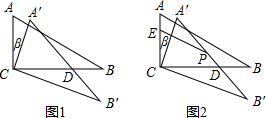
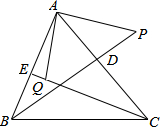 如图,BD,CE分别是△ABC的边AC,AB上的高线,点P在BD的延长线上,BP=AC;点Q在CE上,CQ=BA,猜想AP和AQ的关系,并证明你的猜想.
如图,BD,CE分别是△ABC的边AC,AB上的高线,点P在BD的延长线上,BP=AC;点Q在CE上,CQ=BA,猜想AP和AQ的关系,并证明你的猜想.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
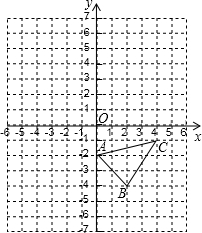 已知:如图,已知△ABC中,其中A(0,-2),B(2,-4),C(4,-1).
已知:如图,已知△ABC中,其中A(0,-2),B(2,-4),C(4,-1).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com