
| 运动鞋价格 | 甲 | 乙 |
| 进价(元/双) | m | m-20 |
| 售价(元/双) | 240 | 160 |
分析 (1)用总价除以单价表示出购进鞋的数量,根据两种鞋的数量相等列出方程求解即可;
(2)设购进甲种运动鞋x双,表示出乙种运动鞋(200-x)双,然后根据总利润列出一元一次不等式,求出不等式组的解集后,再根据鞋的双数是正整数解答即可.
解答 .解:(1)依题意得 $\frac{3600}{m}=\frac{3000}{m-2}$,
整理得,3600(m-2)=3000m,
解得m=120,
经检验,m=120是原分式方程的解,
所以,m=120;
(2)设购进甲种运动鞋x双,则乙种运动鞋(200-x)双,
根据题意得,$\left\{\begin{array}{l}{(240-120)x+(160-100)(200-x)≥21600}\\{(240-120)x+(160-100)(200-x)≤22440}\end{array}\right.$,
不等式组的解集是160≤x≤174,
∵x是正整数,174-160+1=15,
∴共有15种方案.
点评 本题考查了分式方程的应用,一元一次不等式组的应用,解决问题的关键是读懂题意,找到关键描述语,进而找到所求的量的等量关系和不等关系,解决问题.


 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案科目:初中数学 来源: 题型:解答题
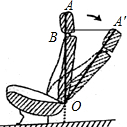 如图,这是一把可调节座椅的侧面示意图,已知头枕上的点A到调节器点O处的距离为80cm,AO与地面垂直,现调整靠背,把OA绕点O顺时针旋转35°到OA′处,此时点A′到OA的距离为线段A′B的长,求调整后点A′比调整前点A降低的高度AB.(结果取整数)【参考数据:sin35°≈0.57,cos35°≈0.82,tan35°≈0.70】
如图,这是一把可调节座椅的侧面示意图,已知头枕上的点A到调节器点O处的距离为80cm,AO与地面垂直,现调整靠背,把OA绕点O顺时针旋转35°到OA′处,此时点A′到OA的距离为线段A′B的长,求调整后点A′比调整前点A降低的高度AB.(结果取整数)【参考数据:sin35°≈0.57,cos35°≈0.82,tan35°≈0.70】查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
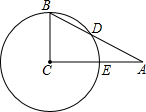 如图,在Rt△ABC中,∠C=90°,∠A=20°,BC=3,以点C为圆心,BC的长为半径的⊙C交AB于点D,交AC于点E,则$\widehat{BD}$(劣弧)的长为( )
如图,在Rt△ABC中,∠C=90°,∠A=20°,BC=3,以点C为圆心,BC的长为半径的⊙C交AB于点D,交AC于点E,则$\widehat{BD}$(劣弧)的长为( )| A. | $\frac{2}{3}$π | B. | $\frac{3}{5}$π | C. | $\frac{1}{3}$π | D. | $\frac{3}{4}$π |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
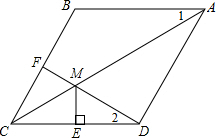 已知:如图,在菱形ABCD中,F为边BC的中点,DF与对角线AC交于点M,过M作ME⊥CD于点E,∠1=∠2.
已知:如图,在菱形ABCD中,F为边BC的中点,DF与对角线AC交于点M,过M作ME⊥CD于点E,∠1=∠2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com