
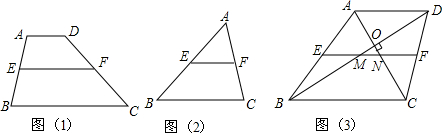
分析 (1)由AD∥BC且∠DBC=30°可知∠ADC=30°,OA=$\frac{1}{2}$AD;同理可得出OC=$\frac{1}{2}$BC;由AC=OA+OC=$\frac{1}{2}$(AD+BC)结合给定的材料一即可证明结论成立;
(2)结合(1)可知OA=$\frac{1}{2}$AD,OC=$\frac{1}{2}$BC,在直角△AOD中由已知条件可求出OA的长度,根据边与边之间的关系可得出线段ON的长度,由MN∥AD可得出∠OMN=30°,MN=2ON,代入ON的长度即可得出结论.
解答 (1)证明:∵AD∥BC,
∴∠ADO=∠DBC=30°.
在Rt△AOD中,∠ADO=30°,
∴OA=$\frac{1}{2}$AD.
同理:OC=$\frac{1}{2}$BC.
∴AC=OA+OC=$\frac{1}{2}$AD+$\frac{1}{2}$BC=$\frac{1}{2}$(AD+BC).
∵E、F分别为AB、CD的中点,
∴EF=$\frac{1}{2}$(AD+BC),
∴EF=AC.
(2)解:由(1)得:在Rt△AOD和Rt△BOC中,OA=$\frac{1}{2}$AD,OC=$\frac{1}{2}$BC,
∵OD=3$\sqrt{3}$,OC=5,
∴OA=OD•tan30°=3.
∵AD∥EF,
∴∠ADO=∠OMN=30°,
∴ON=$\frac{1}{2}$MN.
∵EF∥BC,且E为线段AB中点,
∴EN为△ABC中位线,
∴AN=$\frac{1}{2}$AC=$\frac{1}{2}$(OA+OC)=4,
∴ON=AN-OA=4-3=1,
∴MN=2ON=2.
点评 本题考查了梯形中位线的性质、平行线的性质、三角形中位线定理以及特殊角的三角函数,解题的关键:(1)找出AC=OA+OC=$\frac{1}{2}$(AD+BC);(2)根据边角关系求出ON的长度.本题属于中档题,难度不大,解决该类型题目时,利用给定材料中梯形中位线的性质结合边角关系寻找相等的量.


科目:初中数学 来源: 题型:解答题
| 运动鞋价格 | 甲 | 乙 |
| 进价(元/双) | m | m-20 |
| 售价(元/双) | 240 | 160 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| 年龄(岁) | 11 | 12 | 13 | 14 | 15 |
| 人数 | 3 | 3 | 7 | 12 | 14 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 12 | B. | 0.3 | C. | 0.4 | D. | 40 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
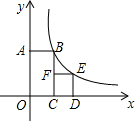 如图,四边形OABC是矩形,四边形CDEF是正方形,点C,D在x轴的正半轴上,点A在y轴的正半轴上,点F在BC上,点B,E在反比例函数y=$\frac{k}{x}$的图象上,OA=2,OC=1,则正方形CDEF的面积为( )
如图,四边形OABC是矩形,四边形CDEF是正方形,点C,D在x轴的正半轴上,点A在y轴的正半轴上,点F在BC上,点B,E在反比例函数y=$\frac{k}{x}$的图象上,OA=2,OC=1,则正方形CDEF的面积为( )| A. | 4 | B. | 1 | C. | 3 | D. | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com