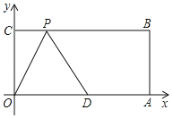
【题目】如图，在平面直角坐标系中，O为坐标原点，四边形OABC是长方形，点A、C的坐标分别为A（10，0）、C（0，4），点D是OA的中点，点P在BC边上运动，当△ADP为等腰三角形时，点P的坐标为_______________________________．
【答案】(2，4)，(8，4)，(7，4)，(7.5，4)
【解析】
分PD=DA，AD=PA，DP=PA三种情况讨论，再根据勾股定理求P点坐标
当PD=DA
如图：以D为圆心AD长为半径作圆，与BD交P点，P'点，过P点作PE⊥OA于E点，过P'点作P'F⊥OA于F点，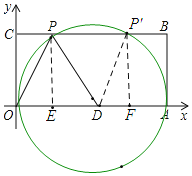
∵四边形OABC是长方形，点A、C的坐标分别为A（10，0）、C（0，4），
∴AD=PD=5，PE=P'F=4
∴根据勾股定理得：DE=DF=
∴P（2，4），P'（8，4）
若AD=AP=5，同理可得：P（7，4）
若PD=PA，则P在AD的垂直平分线上，
∴P（7.5，4）
故答案为：（2，4），（8，4），（7，4），（7.5，4）
课堂练加测系列答案
轻松课堂单元测试AB卷系列答案科目：初中数学 来源： 题型：
【题目】如图，已知小正方形ABCD的面积为1，把它的各边延长一倍得到新正方形A1B1C1D1；把正方形A1B1C1D1边长按原法延长一倍得到正方形A2B2C2D2；以此进行下去…，则正方形A2019B2019C2019D2019的面积为（ ）
A.52017B.52018C.52019D.52020
查看答案和解析>>
科目：初中数学 来源： 题型：
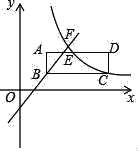
【题目】如图，矩形ABCD在平面直角坐标系的第一象限内，BC与x轴平行，AB=1，点C的坐标为（6，2），E是AD的中点；反比例函数y1=
（x＞0）图象经过点C和点E，过点B的直线y2=ax+b与反比例函数图象交于点F，点F的纵坐标为4．
（1）求反比例函数的解析式和点E的坐标；
（2）求直线BF的解析式；
（3）直接写出y1＞y2时，自变量x的取值范围．
查看答案和解析>>
科目：初中数学 来源： 题型：
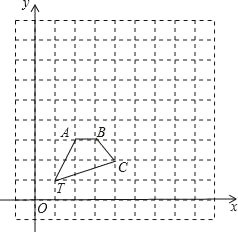
【题目】如图，在正方形网格中，四边形TABC的顶点坐标分别为T（1，1），A（2，3），B（3，3），C（4，2）．
(1)以点T（1，1）为位似中心，在位似中心的同侧将四边形TABC放大为原来的2倍，放大后点A，B，C的对应点分别为A′，B′，C′画出四边形TA′B′C′；
(2)写出点A′，B′，C′的坐标：
A′ ，B′ ，C′ ；
(3)在(1)中，若D（a，b）为线段AC上任一点，则变化后点D的对应点D′的坐标为 ．
查看答案和解析>>
科目：初中数学 来源： 题型：
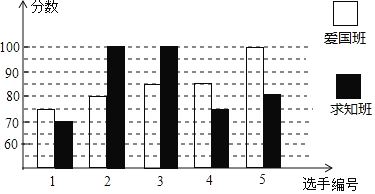
【题目】某校初二开展英语拼写大赛，爱国班和求知班根据初赛成绩，各选出5名选手参加复赛，两个班各选出的5名选手的复赛成绩如图所示：
（1）根据图示填写下表：
班级 | 中位数（分） | 众数（分） | 平均数（分） |
爱国班 | 85 | ||
求知班 | 100 | 85 |
（2）结合两班复赛成绩的平均数和中位数，分析哪个班级的复赛成绩比较好？
（3）已知爱国班复赛成绩的方差是70，请求出求知班复赛成绩的方差，并说明哪个班成绩比较稳定？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在大课间活动中，同学们积极参加体育锻炼，小龙在全校随机抽取了一部分同学就“我最喜爱的体育项目”进行了一次调查（每位同学必选且只选一项）．下面是他通过收集的数据绘制的两幅不完整的统计图，请你根据图中提供的信息，解答以下问题：
（1）小龙一共抽取了 名学生．
（2）补全条形统计图；
（3）求“其他”部分对应的扇形圆心角的度数．
查看答案和解析>>
科目：初中数学 来源： 题型：
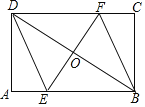
【题目】如图，在矩形ABCD中，BD的垂直平分线分别交AB、CD、BD于E、F、O，连接DE、BF．
（1）求证：四边形BEDF是菱形；
（2）若AB=16cm，BC=8cm，求四边形DEBF的面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
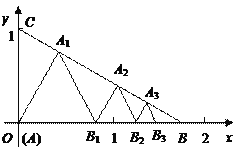
【题目】如图所示，已知：点A(0，0)，B（
，0），C（0，1）在△ABC内依次作等边三角形，使一边在x轴上，另一个顶点在BC边上，作出的等边三角形分别是第1个△AA1B1，第2个△B1A2B2，第3个△B2A3B3，…，则第
个等边三角形的边长等于__________．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
