
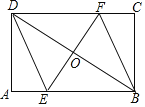
【题目】如图,在矩形ABCD中,BD的垂直平分线分别交AB、CD、BD于E、F、O,连接DE、BF.
(1)求证:四边形BEDF是菱形;
(2)若AB=16cm,BC=8cm,求四边形DEBF的面积.
【答案】(1)详见解析;(2)80(cm2)
【解析】
(1)由题意得出∠OBE=∠ODF,由BD的垂直平分线得出OB=OD,证得△BOE≌△DOF,得出OE=OF,推出四边形BEDF是平行四边形,再由EF垂直平分BD,得出BE=DE,即可得出结论;
(2)由矩形、菱形的性质与勾股定理解得:BE=10cm,即可得出结果.
(1)证明:∵四边形ABCD是矩形,
∴∠A=90°,AD=BC,AB∥DC,
∴∠OBE=∠ODF,
∵BD的垂直平分线分别交AB、CD、BD于E、F、O,
∴OB=OD,
在△BOE和△DOF中,
 ,
,
∴△BOE≌△DOF(ASA),
∴OE=OF,
∵OB=OD,
∴四边形BEDF是平行四边形,
∵EF垂直平分BD,
∴BE=DE,
∴四边形BEDF是菱形;
(2)解∵四边形ABCD是矩形,
∴AD=BC=8cm,AE=AB-BE=16-BE,
∵BE=DE,在Rt△DAE中,DE2=AD2+AE2,
即BE2=82+(16-BE)2,
解得:BE=10(cm),
∴四边形DEBF的面积=ADBE=8×10=80(cm2)


 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案科目:初中数学 来源: 题型:
【题目】重庆李子坝轻轨站穿楼而过成网红,小明想要测量轻轨站穿楼时轨道与大楼连接处![]() 距离地面
距离地面![]() 的高度,他站在点
的高度,他站在点![]() 处测得轨道与大楼连接处顶端
处测得轨道与大楼连接处顶端![]() 的仰角为
的仰角为![]() ,向前走了
,向前走了![]() 米到达
米到达![]() 处,再沿着坡度为
处,再沿着坡度为![]() ,长度为
,长度为![]() 米台阶到达
米台阶到达![]() 处,测得轨道与大楼连接处顶端
处,测得轨道与大楼连接处顶端![]() 的仰角为
的仰角为![]() ,已知小明的身高为
,已知小明的身高为![]() 米,则
米,则![]() 的高度约为( )米(精确到
的高度约为( )米(精确到![]() ,参考数据:
,参考数据:![]() ,
,![]() ,
,![]() )
)
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
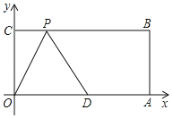
【题目】如图,在平面直角坐标系中,O为坐标原点,四边形OABC是长方形,点A、C的坐标分别为A(10,0)、C(0,4),点D是OA的中点,点P在BC边上运动,当△ADP为等腰三角形时,点P的坐标为_______________________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
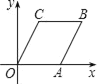
【题目】如图,在平面直角坐标系中,OABC的顶点A在x轴上,顶点B的坐标为(6,4).若直线l经过点(1,0),且将OABC分割成面积相等的两部分,则直线l的函数解析式是( )
A. y=x+1B. ![]() C. y=3x﹣3D. y=x﹣1
C. y=3x﹣3D. y=x﹣1
查看答案和解析>>
科目:初中数学 来源: 题型:
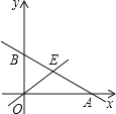
【题目】如图,直线y=-![]() x+b与x轴交于点A,与y轴交于点B,与直线y=x交于点E,点E的横坐标为3.
x+b与x轴交于点A,与y轴交于点B,与直线y=x交于点E,点E的横坐标为3.
(1)求点E的坐标和b的值;
(2)在x轴上有点P(m,0),过点P作x轴的垂线,与直线y=-![]() x+b交于点C,与直线y=x交于点D.若CD≤4,求m的取值范围.
x+b交于点C,与直线y=x交于点D.若CD≤4,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC中,∠A,∠B,∠C的对边分别记为![]() ,
,![]() ,
,![]() ,由下列条件不能判定△ABC为直角三角形的是( ).
,由下列条件不能判定△ABC为直角三角形的是( ).
A.∠A+∠B=∠C
B.∠A∶∠B∶∠C =1∶2∶3
C.![]()
D.![]() ∶
∶![]() ∶
∶![]() =3∶4∶6
=3∶4∶6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两公司为“见义勇为基金会”各捐款3000元.已知甲公司的人数比乙公司的人数多20%,乙公司比甲公司人均多捐20元.请你根据上述信息,就这两个公司的“人数”或“人均捐款”提出一个用分式方程解决的题,并写出解题过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,D为⊙O上一点,过弧BD上一点T作⊙O的切线TC,且TC⊥AD于点C.
(1)若∠DAB=50°,求∠ATC的度数;
(2)若⊙O半径为2,TC=![]() ,求AD的长.
,求AD的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com