
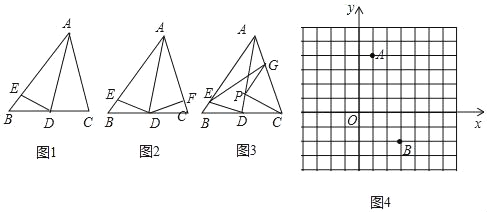
【题目】将纸片△ABC沿AD折叠,使点C刚好落在AB边上的E处,展开如图1.
[操作观察]
(1)如图2,作DF⊥AC,垂足为F,且DF=3,AC=6,S△ABC=21,则AB= ;
[理解应用]
(2)①如图3,设G为AC上一点(与A、C)不重合,P是AD上一个动点,连接PG、PC.试说明:PG+PC与EG大小关系;
②连接EC,若∠BAC=60°,G为AC中点,且AC=6,求EC长.
[拓展延伸]
(3)请根据前面的解题经验,解决下面问题:
如图4,在平面直角坐标系中有A(1,4),B(3,﹣2),点P是x轴上的动点,连接AP、BP,当AP﹣BP的值最大时,请在图中标出P点的位置,并直接写出此时P点的坐标为 ,AP﹣BP的最大值为 .
【答案】(1)8;(2)①PG+PC≥EG,理由见解析;②连6;(3)(5,0),2![]() .
.
【解析】
(1)根据折叠的特性可知折痕AD为∠BAC的角平分线,由此可得出点D到AB和点D到AC的距离相等,再根据三角形的面积公式即可得出结论;
(2)连接CM、PE、CE,根据三角形两边之和大于第三边得出当点P与点M重合时,PF+PC值最小,再根据折叠的性质得出AE=AC,结合∠BAC=60°即可得出△AEC为等边三角形,由此即可解决问题;
(3)作点B关于x轴的对称点B′,连接AB′、PB′,延长AB′交x轴于点P′,根据三角形内两边之差小于第三边找出当点P和P′点重合时,AP﹣BP的值最大,再由点B的坐标可得出点B′的坐标,结合点A、B′的坐标即可求出直线AB′的解析式,令其y=0求出x即可找出点P′的坐标,由此即可得出结论.
(1)∵将纸片△ABC沿AD折叠,使C点刚好落在AB边上的E处,∴AD为∠BAC的角平分线,∴点D到AB和点D到AC的距离相等,∴S△ABC=![]() ABDF+
ABDF+![]() ACDF=21,∴
ACDF=21,∴![]() AB3+
AB3+![]() ×6×3=21,∴AB=8.
×6×3=21,∴AB=8.
故答案为:8.
(2)①结论:PG+PC≥EG.理由如下:
连接PE,如图3所示.

∵将纸片△ABC沿AD折叠,使C点刚好落在AB边上的E处,∴AD为∠BAC的角平分线,AE=AC,∴PE=PC.在△PEG中,PE+PG≥EG,∴PC+PG≥EG.
②连接EC,如图3中.
∵AE=AC,∠BAC=60°,∴△AEC为等边三角形.
又∵AC=6,∴EC=AC=6.
(3)作点B关于x轴的对称点B′,连接AB′、PB′,延长AB′交x轴于点P′,如图4所示.

∵点B和B′关于x轴对称,∴PB=PB′,P′B′=P′B.
∵在△APB′中,AB′>AP﹣PB′,∴AP′﹣B′P′=AP′﹣BP′=AB′>AP﹣PB′=AP﹣PB,∴当点P与点P′重合时,AP﹣BP最大.
设直线AB′的解析式为y=kx+b.
∵点B(3,﹣2),∴点B′(3,2),AB′=![]() =
=![]() =2
=2![]() .
.
将点A(1,4)、B′(3,2)代入y=kx+b中,得:![]() ,解得:
,解得:![]() ,∴直线AB′的解析式为y=﹣x+5.
,∴直线AB′的解析式为y=﹣x+5.
令y=﹣x+5中y=0,则﹣x+5=0,解得:x=5,∴点P′(5,0).
故AP﹣BP的最大值为2![]() ,此时P点的坐标为(5,0).
,此时P点的坐标为(5,0).
故答案为:(5,0),2![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,在等腰三角形ABC中,AB=AC,以底边BC的垂直平分线和BC所在的直线建立平面直角坐标系,抛物线y=﹣ ![]() x2+
x2+ ![]() x+4经过A、B两点.
x+4经过A、B两点.
(1)写出点A、点B的坐标;
(2)若一条与y轴重合的直线l以每秒2个单位长度的速度向右平移,分别交线段OA、CA和抛物线于点E、M和点P,连接PA、PB.设直线l移动的时间为t(0<t<4)秒,求四边形PBCA的面积S(面积单位)与t(秒)的函数关系式,并求出四边形PBCA的最大面积;
(3)在(2)的条件下,抛物线上是否存在一点P,使得△PAM是直角三角形?若存在,请求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC,且∠ACB=90°.
(1)请用直尺和圆规按要求作图(保留作图痕迹,不写作法和证明):
①以点A为圆心,BC边的长为半径作⊙A;
②以点B为顶点,在AB边的下方作∠ABD=∠BAC.
(2)请判断直线BD与⊙A的位置关系(不必证明).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(5分)已知A,B两地相距200千米,一辆汽车以每小时60千米的速度从A地匀速驶往B地,到达B地后不再行驶,设汽车行驶的时间为x小时,汽车与B地的距离为y千米.
(1)求y与x的函数关系,并写出自变量x的取值范围;
(2)当汽车行驶了2小时时,求汽车距B地有多少千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在下列条件中,不能作为判断△ABD≌△BAC的条件是( )

A. ∠D=∠C,∠BAD=∠ABC B. ∠BAD=∠ABC,∠ABD=∠BAC
C. BD=AC,∠BAD=∠ABC D. AD=BC,BD=AC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点A,B的坐标分别为(-2,3)和(1,3),抛物线y=ax2+bx+c(a<0)的顶点在线段AB上运动时,形状保持不变,且与x轴交于C,D两点(C在D的左侧),给出下列结论:①c<3;②当x<-3时,y随x的增大而增大;③若点D的横坐标最大值为5,则点C的横坐标最小值为-5;④当四边形ACDB为平行四边形时,a= ![]() .其中正确的是( )
.其中正确的是( )
A.②④
B.②③
C.①③④
D.①②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程解应用题:

在元旦放假期间,小张、小王等同学跟随家长一起到公园游玩,下面是购买门票时小张和爸爸的对话:

![]()

请根据图中的信息解答问题:
(1)他们中一共有成年人多少人?学生多少人?
(2)请你帮助小张算一算,用哪种方式购票更省钱并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
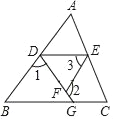
【题目】如图,已知,∠3=∠B,∠1+∠2=180°,∠AED=∠C大小相等吗?请说明理由.
请完成填空并补充完整.
解:因为∠1+∠2=180°(已知)
又因为∠2+∠ =180°(邻补角的意义)
所以∠1=∠ ( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下图可以近似地刻画下列哪个情景( )
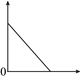
A. 小明匀速步行上学时离学校的距离与时间的关系
B. 匀速行驶的汽车的速度与时间的关系
C. 小亮妈妈到超市购买苹果的总费用与苹果质量的关系
D. 一个匀速上升的气球的高度与时间的关系
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com