
���� ��1���ҳ����ã�60-x����ԭ��������A��Ʒ��
��2���׳�����x��ԭ��������A��Ʒ�����ҳ����ã�60-x����ԭ��������A��Ʒ���н�ɣ�
��3����׳�����x��ԭ��������A��Ʒ���г����̽�ɣ�
��4����������=��Ʒ���ۼ�-����ԭ���ϳɱ�-ˮ���г�����ʽ��ɣ�
��� �⣺��1���ҳ����ã�60-x����ԭ��������A��Ʒ��
�ʴ�Ϊ����60-x����
��2����������������A��Ʒ���ܺ�ˮΪΪ4x+2��60-x��=2x+120��
�ʴ�Ϊ��2x+120��
��3����׳�����x��ԭ��������A��Ʒ���ɵã�2x+120=200��
��ã�x=40��
�𣺼׳�����40��ԭ��������A��Ʒ��
��4����������ɵã�30[12x+10��60-x��]-80��60-5[4x+2��60-x��]=50x+12600��
���� ���⿼�����д���ʽ���������Ĺؼ��Ǹ��������г���ϵʽ�����ô���ʽ������⣮


 ͬ��������ϰϵ�д�
ͬ��������ϰϵ�д� �ο�ͨ�γ̱�˼ά����������ѵ��ϵ�д�
�ο�ͨ�γ̱�˼ά����������ѵ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -33=-9 | B�� | 3x2y-2yx2=x2y | C�� | 6a-5a=1 | D�� | -2��a-b��=-2a+b |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��������OAB�У���AOB=90�㣬�뾶OA=2��������OAB�ع���B��ֱ���۵�����Oǡ�����ڻ�AB�ϵ�D�����ۺ۽�OA�ڵ�C����������Ӱ���ֵ����Ϊ��-$\frac{4\sqrt{3}}{3}$��
��ͼ��������OAB�У���AOB=90�㣬�뾶OA=2��������OAB�ع���B��ֱ���۵�����Oǡ�����ڻ�AB�ϵ�D�����ۺ۽�OA�ڵ�C����������Ӱ���ֵ����Ϊ��-$\frac{4\sqrt{3}}{3}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ������a��b��c�������ϵ�λ����ͼ��ʾ����|a+b|-2|c-b|+3|b+a|=��������
������a��b��c�������ϵ�λ����ͼ��ʾ����|a+b|-2|c-b|+3|b+a|=��������| A�� | -2b | B�� | 0 | C�� | -4a-b-3c | D�� | -4a-2b-2c |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
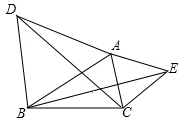 ��ͼ���ֱ�ӡ�ABC�ı�AB��ACΪһ���������ȱ�������ABD��ACE������BE��DC��BE��DC�������˵�����ɣ�
��ͼ���ֱ�ӡ�ABC�ı�AB��ACΪһ���������ȱ�������ABD��ACE������BE��DC��BE��DC�������˵�����ɣ��鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com