
分析 由[$\frac{n}{2}$]+[$\frac{n}{3}$]+[$\frac{n}{6}$]=n,[x]表示不超过x的最大整数,即[x]≤x,知x是6的倍数,自然数n小于2012,所以这样的正整数有[$\frac{2012}{6}$]=335个,但自然数n包括0,0也满足条件,故这样的n共有336个.
解答 解:∵[$\frac{n}{2}$]+[$\frac{n}{3}$]+[$\frac{n}{6}$]=n,
若x不是整数,则[x]<x,
∴$\frac{n}{2}$,$\frac{n}{3}$,$\frac{n}{6}$,即n是6的倍数,
小于2012正整数共有[$\frac{2012}{6}$]=335个,
但自然数n包括0,0也满足条件,
∴这样的n共有336个,
故答案为:336.
点评 本题主要考查了取整函数的意义以及数的整除性,理解题意,不可忽视自然数0是解答此题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
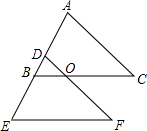 如图所示,△ABC平移后得到△DEF.
如图所示,△ABC平移后得到△DEF.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
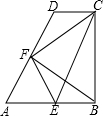 如图,在直角梯形ABCD中,AB∥DC,AB⊥BC,∠A=60°,AB=2CD,E、F分别为AB、AD的中点,连接EF、EC、BF、CF.则①四边形AECD为平行四边形;②△AEF为等边三角形;③△FDC与△BEF为全等的等腰三角形;④△AFB≌△EFC,其中正确的结论有①②③④(写出正确的序号即可)
如图,在直角梯形ABCD中,AB∥DC,AB⊥BC,∠A=60°,AB=2CD,E、F分别为AB、AD的中点,连接EF、EC、BF、CF.则①四边形AECD为平行四边形;②△AEF为等边三角形;③△FDC与△BEF为全等的等腰三角形;④△AFB≌△EFC,其中正确的结论有①②③④(写出正确的序号即可)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
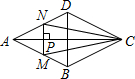 如图,点P是菱形ABCD的对角线AC上的一个动点,过点P垂直于AC的直线交菱形ABCD的边于M、N两点.设AC=2,BD=1,AP=x,△CMN的面积为y,则y关于x的函数图象大致形状是( )
如图,点P是菱形ABCD的对角线AC上的一个动点,过点P垂直于AC的直线交菱形ABCD的边于M、N两点.设AC=2,BD=1,AP=x,△CMN的面积为y,则y关于x的函数图象大致形状是( )| A. | 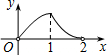 | B. | 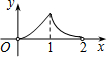 | C. | 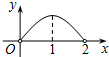 | D. | 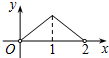 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
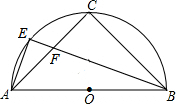 如图,AB是半⊙O的直径,点C是弧AB的中点,点E是弧AC的中点,连结EB、CA交于点F,则$\frac{EF}{BF}$=$\frac{\sqrt{2}-1}{2}$.
如图,AB是半⊙O的直径,点C是弧AB的中点,点E是弧AC的中点,连结EB、CA交于点F,则$\frac{EF}{BF}$=$\frac{\sqrt{2}-1}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
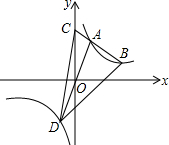 如图,已知直线y=-x+5交双曲线y=$\frac{k}{x}$(x>0)于A、B两点,交y轴于C点,AO的延长线交双曲线y=$\frac{k}{x}$(x<0)于D点,且S△BCD=15,则k=6.
如图,已知直线y=-x+5交双曲线y=$\frac{k}{x}$(x>0)于A、B两点,交y轴于C点,AO的延长线交双曲线y=$\frac{k}{x}$(x<0)于D点,且S△BCD=15,则k=6.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com