
分析 原式通分并利用同分母分式的加减法则计算即可得到结果.
解答 解:原式=$\frac{a+x-a+x}{{a}^{2}-{x}^{2}}$-$\frac{2x}{{a}^{2}+{x}^{2}}$-$\frac{4{x}^{3}}{{a}^{4}+{x}^{4}}$+$\frac{8{x}^{7}}{{x}^{8}-{a}^{8}}$=$\frac{4{x}^{3}}{{a}^{4}-{x}^{4}}$-$\frac{4{x}^{3}}{{a}^{4}+{x}^{4}}$+$\frac{8{x}^{7}}{{x}^{8}-{a}^{8}}$=$\frac{8{x}^{7}}{{a}^{8}-{x}^{8}}$+$\frac{8{x}^{7}}{{x}^{8}-{a}^{8}}$=$\frac{8{x}^{7}-8{x}^{7}}{{a}^{8}-{x}^{8}}$=0.
点评 此题考查了分式的加减法,熟练掌握运算法则是解本题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{99}{97}$ | B. | 98! | C. | 9702 | D. | 2! |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
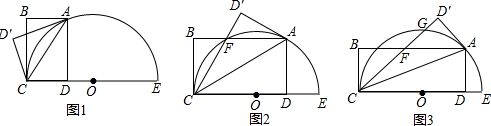
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
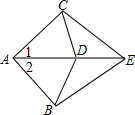 如图,已知AB=AC,BE=CE,D是AE上的一点,则下列结论不一定成立的是( )
如图,已知AB=AC,BE=CE,D是AE上的一点,则下列结论不一定成立的是( )| A. | ∠1=∠2 | B. | AD=DE | C. | BD=CD | D. | ∠BDE=∠CDE |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com