
ĄūĖâÄŋĄŋČįÍž1ĢŽÖąÏßlĢšy=![]() x+mÓëxÖáĄĒyÖá·Öąð―ŧÓÚĩãAšÍĩãBĢĻ0ĢŽĐ1ĢĐĢŽÅŨÎïÏßy=
x+mÓëxÖáĄĒyÖá·Öąð―ŧÓÚĩãAšÍĩãBĢĻ0ĢŽĐ1ĢĐĢŽÅŨÎïÏßy=![]() x2+bx+cūđýĩãBĢŽÓëÖąÏßlĩÄÁíŌŧļö―ŧĩãΊCĢĻ4ĢŽnĢĐĢŪ
x2+bx+cūđýĩãBĢŽÓëÖąÏßlĩÄÁíŌŧļö―ŧĩãΊCĢĻ4ĢŽnĢĐĢŪ
ĢĻ1ĢĐĮónĩÄÖĩšÍÅŨÎïÏßĩÄ―âÎöĘ―Ģŧ
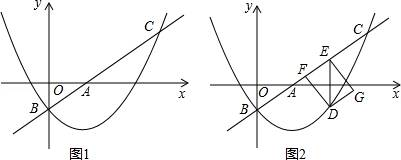
ĢĻ2ĢĐĩãDÔÚÅŨÎïÏßÉÏĢŽDEĄÎyÖá―ŧÖąÏßlÓÚĩãEĢŽĩãFÔÚÖąÏßlÉÏĢŽĮŌËÄąßÐÎDFEGΊūØÐÎĢĻČįÍž2ĢĐĢŽÉčĩãDĩÄšáŨøąęΊtĢĻ0ĢžtĢž4ĢĐĢŽūØÐÎDFEGĩÄÖÜģĪΊpĢŽĮópÓëtĩÄšŊĘýđØÏĩĘ―ŌÔž°pĩÄŨîīóÖĩĢŧ
ĢĻ3ĢĐ―ŦĄũAOBČÆÆ―ÃæÄÚÄģĩãMÐýŨŠ90Ąãŧō180ĄãĢŽĩÃĩ―ĄũA1O1B1ĢŽĩãAĄĒOĄĒBĩÄķÔÓĶĩã·ÖąðĘĮĩãA1ĄĒO1ĄĒB1ĢŪČôĄũA1O1B1ĩÄÁ―ļöķĨĩãĮĄšÃÂäÔÚÅŨÎïÏßÉÏĢŽÄĮÃīÎŌÃĮūÍģÆÕâŅųĩÄĩãΊĄ°ÂäĩãĄąĢŽĮëÖą―ÓÐīģöĄ°ÂäĩãĄąĩÄļöĘýšÍÐýŨŠ180ĄãĘąĩãA1ĩÄšáŨøąęĢŪ
Ąūīð°ļĄŋĢĻ1ĢĐn=2Ģŧy=![]() x2Đ
x2Đ![]() xĐ1ĢŧĢĻ2ĢĐp=
xĐ1ĢŧĢĻ2ĢĐp=![]() Ģŧĩąt=2ĘąĢŽpÓÐŨîīóÖĩ
Ģŧĩąt=2ĘąĢŽpÓÐŨîīóÖĩ![]() ĢŧĢĻ3ĢĐ
ĢŧĢĻ3ĢĐ![]() ŧō
ŧō![]() Ģŧ
Ģŧ
Ąū―âÎöĄŋ
ĢĻ1ĢĐ°ŅĩãBĩÄŨøąęīúČëÖąÏß―âÎöĘ―ĮóģömĩÄÖĩĢŽÔŲ°ŅĩãCĩÄŨøąęīúČëÖąÏßĮó―âžīŋÉĩÃĩ―nĩÄÖĩĢŽČŧšóĀûÓÃīýķĻÏĩĘý·ĻĮóķþīΚŊĘý―âÎöĘ――âīðĢŧ
ĢĻ2ĢĐÁîy=0ĮóģöĩãAĩÄŨøąęĢŽīÓķøĩÃĩ―OAĄĒOBĩÄģĪķČĢŽĀûÓÃđīđÉķĻĀíÁÐĘ―ĮóģöABĩÄģĪĢŽČŧšóļųūÝÁ―ÖąÏßÆ―ÐÐĢŽÄÚīí―ĮÏāĩČŋÉĩÃĄÏABO=ĄÏDEFĢŽÔŲ―âÖą―ĮČý―ĮÐÎÓÃDEąíĘūģöEFĄĒDFĢŽļųūÝūØÐÎĩÄÖÜģĪđŦĘ―ąíĘūģöpĢŽĀûÓÃÖąÏßšÍÅŨÎïÏßĩÄ―âÎöĘ―ąíĘūDEĩÄģĪĢŽÕûĀížīŋÉĩÃĩ―PÓëtĩÄđØÏĩĘ―ĢŽÔŲĀûÓÃķþīΚŊĘýĩÄŨîÖĩÎĘĖâ―âīðĢŧ
ĢĻ3ĢĐļųūÝÄæĘąÕëÐýŨŠ―ĮΊ90ĄãŋÉĩÃA1O1ĄÎyÖáĘąĢŽB1O1ĄÎxÖáĢŽÐýŨŠ―ĮĘĮ180ĄãÅÐķÏģöA1O1ĄÎxÖáĘąĢŽB1A1ĄÎABĢŽļųūÝÍž3ĄĒÍž4Á―ÖÖĮéÐΞīŋÉ―âūöĢŪ
―âĢš
ĢĻ1ĢĐĄßÖąÏßlĢšy=![]() x+mūđýĩãBĢĻ0ĢŽĐ1ĢĐĢŽ
x+mūđýĩãBĢĻ0ĢŽĐ1ĢĐĢŽ
Ąām=Đ1ĢŽ
ĄāÖąÏßlĩÄ―âÎöĘ―ÎŠy=![]() xĐ1ĢŽ
xĐ1ĢŽ
ĄßÖąÏßlĢšy=![]() xĐ1ūđýĩãCĢĻ4ĢŽnĢĐĢŽ
xĐ1ūđýĩãCĢĻ4ĢŽnĢĐĢŽ
Ąān=![]() ĄÁ4Đ1=2ĢŽ
ĄÁ4Đ1=2ĢŽ
ĄßÅŨÎïÏßy=![]() x2+bx+cūđýĩãCĢĻ4ĢŽ2ĢĐšÍĩãBĢĻ0ĢŽĐ1ĢĐĢŽ
x2+bx+cūđýĩãCĢĻ4ĢŽ2ĢĐšÍĩãBĢĻ0ĢŽĐ1ĢĐĢŽ
Ąā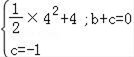 ĢŽ
ĢŽ
―âĩÃ![]() ĢŽ
ĢŽ
ĄāÅŨÎïÏßĩÄ―âÎöĘ―ÎŠy=![]() x2Đ
x2Đ![]() xĐ1Ģŧ
xĐ1Ģŧ
ĢĻ2ĢĐÁîy=0ĢŽÔō![]() xĐ1=0ĢŽ
xĐ1=0ĢŽ
―âĩÃx=![]() ĢŽ
ĢŽ
ĄāĩãAĩÄŨøąęΊĢĻ![]() ĢŽ0ĢĐĢŽ
ĢŽ0ĢĐĢŽ
ĄāOA=![]() ĢŽ
ĢŽ
ÔÚRtĄũOABÖÐĢŽOB=1ĢŽ
ĄāAB=![]() =
=![]() =
=![]() ĢŽ
ĢŽ
ĄßDEĄÎyÖáĢŽ
ĄāĄÏABO=ĄÏDEFĢŽ
ÔÚūØÐÎDFEGÖÐĢŽEF=DEcosĄÏDEF=DE![]() =
=![]() DEĢŽ
DEĢŽ
DF=DEsinĄÏDEF=DE![]() =
=![]() DEĢŽ
DEĢŽ
Ąāp=2ĢĻDF+EFĢĐ=2ĢĻ![]() +
+![]() ĢĐDE=
ĢĐDE=![]() DEĢŽ
DEĢŽ
ĄßĩãDĩÄšáŨøąęΊtĢĻ0ĢžtĢž4ĢĐĢŽ
ĄāDĢĻtĢŽ![]() t2Đ
t2Đ![]() tĐ1ĢĐĢŽEĢĻtĢŽ
tĐ1ĢĐĢŽEĢĻtĢŽ![]() tĐ1ĢĐĢŽ
tĐ1ĢĐĢŽ
ĄāDE=ĢĻ![]() tĐ1ĢĐĐĢĻ
tĐ1ĢĐĐĢĻ![]() t2Đ
t2Đ![]() tĐ1ĢĐ=Đ
tĐ1ĢĐ=Đ![]() t2+2tĢŽ
t2+2tĢŽ
Ąāp=![]() ĄÁĢĻĐ
ĄÁĢĻĐ![]() t2+2tĢĐ=Đ
t2+2tĢĐ=Đ![]() t2+
t2+![]() tĢŽ
tĢŽ
Ąßp=Đ![]() ĢĻtĐ2ĢĐ2+
ĢĻtĐ2ĢĐ2+![]() ĢŽĮŌĐ
ĢŽĮŌĐ![]() Ģž0ĢŽ
Ģž0ĢŽ
Ąāĩąt=2ĘąĢŽpÓÐŨîīóÖĩ![]() ĢŪ
ĢŪ
ĢĻ3ĢĐĄ°ÂäĩãĄąĩÄļöĘýÓÐ6ļöĢŽČįÍž1ĢŽÍž2ÖÐļũÓÐ2ļöĢŽÍž3ĢŽÍž4ļũÓÐŌŧļöËųĘūĢŪ
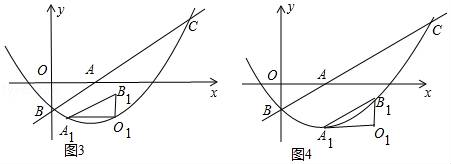
ČįÍž3ÖÐĢŽÉčA1ĩÄšáŨøąęΊmĢŽÔōO1ĩÄšáŨøąęΊm+![]() ĢŽ
ĢŽ
Ąā![]() m2Đ
m2Đ![]() mĐ1=
mĐ1=![]() ĢĻm+
ĢĻm+![]() ĢĐ2Đ
ĢĐ2Đ![]() ĢĻm+
ĢĻm+![]() ĢĐĐ1ĢŽ
ĢĐĐ1ĢŽ
―âĩÃm=![]() ĢŽ
ĢŽ
ČįÍž4ÖÐĢŽÉčA1ĩÄšáŨøąęΊmĢŽÔōB1ĩÄšáŨøąęΊm+![]() ĢŽB1ĩÄŨÝŨøąęąČĀýA1ĩÄŨÝŨøąęīó1ĢŽ
ĢŽB1ĩÄŨÝŨøąęąČĀýA1ĩÄŨÝŨøąęīó1ĢŽ
Ąā![]() m2Đ
m2Đ![]() mĐ1+1=
mĐ1+1=![]() ĢĻm+
ĢĻm+![]() ĢĐ2Đ
ĢĐ2Đ![]() ĢĻm+
ĢĻm+![]() ĢĐĐ1ĢŽ
ĢĐĐ1ĢŽ
―âĩÃm=![]() ĢŽ
ĢŽ
ĄāÐýŨŠ180ĄãĘąĩãA1ĩÄšáŨøąęΊ![]() ŧō
ŧō![]()



| Äęžķ | ļßÖÐŋÎģĖ | Äęžķ | ģõÖÐŋÎģĖ |
| ļßŌŧ | ļßŌŧÃâ·ŅŋÎģĖÍÆžöĢĄ | ģõŌŧ | ģõŌŧÃâ·ŅŋÎģĖÍÆžöĢĄ |
| ļßķþ | ļßķþÃâ·ŅŋÎģĖÍÆžöĢĄ | ģõķþ | ģõķþÃâ·ŅŋÎģĖÍÆžöĢĄ |
| ļßČý | ļßČýÃâ·ŅŋÎģĖÍÆžöĢĄ | ģõČý | ģõČýÃâ·ŅŋÎģĖÍÆžöĢĄ |
ŋÆÄŋĢšģõÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢš
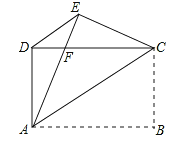
ĄūĖâÄŋĄŋČįÍžĢŽūØÐÎ![]() ÖÐĢŽ
ÖÐĢŽ![]() ĢŽ°ŅūØÐÎŅØķÔ―ĮÏß
ĢŽ°ŅūØÐÎŅØķÔ―ĮÏß![]() ËųÔÚÖąÏßÕÛĩþĢŽĘđĩã
ËųÔÚÖąÏßÕÛĩþĢŽĘđĩã![]() ÂäÔÚĩã
ÂäÔÚĩã![]() īĶĢŽ
īĶĢŽ![]() ―ŧ
―ŧ![]() ÓÚĩã
ÓÚĩã![]() ĢŽÁŽ―Ó
ĢŽÁŽ―Ó![]() ĢŪ
ĢŪ
ĢĻ1ĢĐĮóÖĪĢš![]() Ģŧ
Ģŧ
ĢĻ2ĢĐĮóÖĪĢš![]() ĘĮĩČŅüČý―ĮÐÎĢŪ
ĘĮĩČŅüČý―ĮÐÎĢŪ
ēéŋīīð°ļšÍ―âÎö>>
ŋÆÄŋĢšģõÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢš
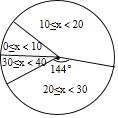
ĄūĖâÄŋĄŋĖåÓýŨéΊÁËÁË―âūÅÄęžķ450ÃûŅ§ÉúÅÅĮōĩæĮōĩÄĮéŋöĢŽËæŧúģéēéÁËūÅÄęžķēŋ·ÖŅ§Éú―øÐÐÅÅĮōĩæĮōēâĘÔĢĻĩĨÎŧĢšļöĢĐĢŽļųūÝēâĘÔ―áđûĢŽÖÆģÉÁËÏÂÃæēŧÍęÕûĩÄÍģžÆÍžąíĢš
Ũéąð | ļöĘýķÎ | ÆĩĘý | ÆĩÂĘ |
1 |
| 5 | 0.1 |
2 |
| 21 | 0.42 |
3 |
|
| |
4 |
|
|
ĢĻ1ĢĐąíÖÐĩÄĘý![]() ĄĄ ĄĄĢŽ
ĄĄ ĄĄĢŽ![]() ĄĄ ĄĄĢŧ
ĄĄ ĄĄĢŧ
ĢĻ2ĢĐđĀËãļÃūÅÄęžķÅÅĮōĩæĮōēâĘÔ―áđûÐĄÓÚ10ĩÄČËĘýĢŧ
ĢĻ3ĢĐÅÅĮōĩæĮōēâĘÔ―áđûÐĄÓÚ10ĩÄΊēŧīïąęĢŽČôēŧīïąęĩÄ5ČËÖÐÓÐ3ļöÄÐÉúĢŽ2ļöÅŪÉúĢŽÏÖīÓÕâ5ČËÖÐËæŧúŅĄģö2ČËĩũēéĢŽĘÔÍĻđýŧĘũŨīÍžŧōÁÐąíĩÄ·―·ĻĮóŅĄģöĩÄ2ČËΊŌŧļöÄÐÉúŌŧļöÅŪÉúĩÄļÅÂĘĢŪ
ēéŋīīð°ļšÍ―âÎö>>
ŋÆÄŋĢšģõÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢš
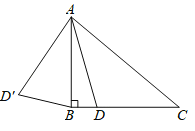
ĄūĖâÄŋĄŋČįÍžĢŽÔÚRtĄũABCÖÐĢŽĄÏABCĢ―90ĄãĢŽĄÏCĢ―30ĄãĢŽĩãDĘĮÏßķÎBCÉÏĩÄķŊĩãĢŽ―ŦÏßķÎADČÆĩãAËģĘąÕëÐýŨŠ60ĄãÖÁAD'ĢŽÁŽ―ÓBD'ĢŪČôABĢ―2cmĢŽÔōBD'ĩÄŨîÐĄÖĩΊ_____ĢŪ
ēéŋīīð°ļšÍ―âÎö>>
ŋÆÄŋĢšģõÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢš
ĄūĖâÄŋĄŋÅŨÎïÏßy=ax2+bx+3ĢĻaĄŲ0ĢĐđýAĢĻ4ĢŽ4ĢĐĢŽBĢĻ2ĢŽmĢĐÁ―ĩãĢŽĩãBĩ―ÅŨÎïÏßķÔģÆÖáĩÄūāĀëžĮΊdĢŽÂúŨã0ĢždĄÜ1ĢŽÔōĘĩĘýmĩÄČĄÖĩ·ķΧĘĮĢĻĄĄĄĄĢĐ
A. mĄÜ2ŧōmĄÝ3 B. mĄÜ3ŧōmĄÝ4 C. 2ĢžmĢž3 D. 3ĢžmĢž4
ēéŋīīð°ļšÍ―âÎö>>
ŋÆÄŋĢšģõÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢš
ĄūĖâÄŋĄŋČįÍžÔÚÆ―ÃæÖą―ĮŨøąęÏĩÖÐĢŽĄũABCĩÄČýļöķĨĩã·ÖąðΊAĢĻĐ4ĢŽ3ĢĐĢŽBĢĻĐ1ĢŽ2ĢĐĢŽCĢĻĐ2ĢŽ1ĢĐ.
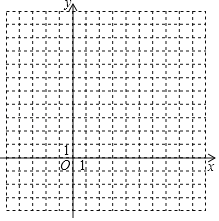
ĢĻ1ĢĐŧģöĄũABCđØÓÚÔĩãOķÔģÆĩÄĄũA1B1C1ĢŽēĒÐīģöĩãA1ĢŽB1ĄĒC1ĩÄŨøąęĢŧ
ĢĻ2ĢĐŧģöĄũABCČÆÔĩãOËģĘąÕë·―ÏōÐýŨŠ90ĄãĩÃĩ―ĩÄĄũA2B2C2ĢŽēĒÐīģöĩãA2ĢŽB2ĢŽC2ĩÄŨøąęĢŪ
ēéŋīīð°ļšÍ―âÎö>>
ŋÆÄŋĢšģõÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢš
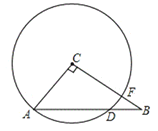
ĄūĖâÄŋĄŋČįÍžĢŽĄũABCÖÐĢŽĄÏC=90ĄãĢŽAC=6,BC=8,ŌÔĩãCΊÔēÐÄĢŽCAĩÄģĪΊ°ëūķĩÄÔēÓëABĄĒBC·ÖąðÏā―ŧÓÚĩãDĄĒFĢŽĮóÔēÐÄĩ―ABĩÄūāĀëž°ADĩÄģĪĢŪ
ēéŋīīð°ļšÍ―âÎö>>
ŋÆÄŋĢšģõÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢš
ĄūĖâÄŋĄŋÔÚÏÂÁÐĩÄÍøļņÍžÖÐ.ÃŋļöÐĄÕý·―ÐÎĩÄąßģĪūųΊ1ļöĩĨÎŧĢŽÔÚRtĄũABCÖÐĢŽĄÏC=90ĄãĢŽAC=3ĢŽBC=4.
(1)ĘÔÔÚÍžÖÐŨũģöĄũABCŌÔAΊÐýŨŠÖÐÐÄĢŽŅØËģĘąÕë·―ÏōÐýŨŠ90ĄãšóĩÄÍžÐÎĄũAB1C1Ģŧ
(2)ČôĩãBĩÄŨøąęΊ(-3ĢŽ5)ĢŽĘÔÔÚÍžÖÐŧģöÖą―ĮŨøąęÏĩĢŽēĒąęģöAĄĒCÁ―ĩãĩÄŨøąęĢŧ
(3)ļųūÝ(2)ÖÐĩÄŨøąęÏĩŨũģöÓëĄũABCđØÓÚÔĩãķÔģÆĩÄÍžÐÎĄũA2B2C2ĢŽēĒąęģöB2ĄĒC2Á―ĩãĩÄŨøąę.

ēéŋīīð°ļšÍ―âÎö>>
ŋÆÄŋĢšģõÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢš
ĄūĖâÄŋĄŋĢĻēŲŨũĖåŅéĢĐ
ČįÍžĒŲĢŽŌŅÖŠÏßķÎABšÍÖąÏßlĢŽÓÃÖąģßšÍÔēđæÔÚlÉÏŨũģöËųÓÐĩÄĩãPĢŽĘđĩÃĄÏAPB=30ĄãĢŽČįÍžĒÚĢŽÐĄÃũĩÄŨũÍž·―·ĻČįÏÂĢš 
ĩÚŌŧē―Ģš·ÖąðŌÔĩãAĢŽBΊÔēÐÄĢŽABģĪΊ°ëūķŨũŧĄĢŽÁ―ŧĄÔÚABÉÏ·――ŧÓÚĩãOĢŧ
ĩÚķþē―ĢšÁŽ―ÓOAĢŽOBĢŧ
ĩÚČýē―ĢšŌÔOΊÔēÐÄĢŽOAģĪΊ°ëūķŨũĄŅOĢŽ―ŧlÓÚ![]() Ģŧ
Ģŧ
ËųŌÔÍžÖÐ![]() žīΊËųĮóĩÄĩãĢŪĢĻ1ĢĐÔÚÍžĒÚÖÐĢŽÁŽ―Ó
žīΊËųĮóĩÄĩãĢŪĢĻ1ĢĐÔÚÍžĒÚÖÐĢŽÁŽ―Ó![]() ĢŽËĩÃũĄÏ
ĢŽËĩÃũĄÏ![]() =30Ąã
=30Ąã
ĢĻ·―·ĻĮĻŌÆĢĐ
ĢĻ2ĢĐČįÍžĒÛĢŽÓÃÖąģßšÍÔēđæÔÚūØÐÎABCDÄÚŨũģöËųÓÐĩÄĩãPĢŽĘđĩÃĄÏBPC=45ĄãĢŽĢĻēŧÐīŨö·ĻĢŽąĢÁôŨũÍžšÛžĢĢĐĢŪ
ĢĻÉîČëĖ―ūŋĢĐ
ĢĻ3ĢĐŌŅÖŠūØÐÎABCDĢŽBC=2ĢŪAB=mĢŽPΊADąßÉÏĩÄĩãĢŽČôÂúŨãĄÏBPC=45ĄãĩÄĩãPĮĄÓÐÁ―ļöĢŽÔōmĩÄČĄÖĩ·ķΧΊ________ĢŪ
ĢĻ4ĢĐŌŅÖŠūØÐÎABCDĢŽAB=3ĢŽBC=2ĢŽPΊūØÐÎABCDÄÚŌŧĩãĢŽĮŌĄÏBPC=135ĄãĢŽČôĩãPČÆĩãAÄæĘąÕëÐýŨŠ90Ąãĩ―ĩãQĢŽÔōPQĩÄŨîÐĄÖĩΊ________ĢŪ
ēéŋīīð°ļšÍ―âÎö>>
đúžĘŅ§ÐĢÓÅŅĄ - Á·Ï°ēáÁÐąí - ĘÔĖâÁÐąí
šþąąĘĄŧĨÁŠÍøÎĨ·ĻšÍēŧÁžÐÅÏĒūŲąĻÆ―ĖĻ | ÍøÉÏÓКĶÐÅÏĒūŲąĻŨĻĮø | ĩįÐÅÕĐÆūŲąĻŨĻĮø | ÉæĀúĘ·ÐéÎÞÖũŌåÓКĶÐÅÏĒūŲąĻŨĻĮø | ÉæÆóĮÖČĻūŲąĻŨĻĮø
ÎĨ·ĻšÍēŧÁžÐÅÏĒūŲąĻĩįŧ°Ģš027-86699610 ūŲąĻÓĘÏäĢš58377363@163.com