
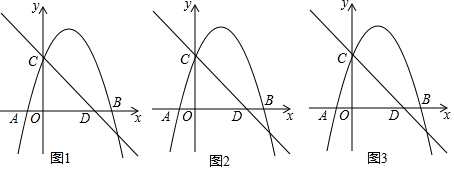
分析 (1)求出点C坐标,利用待定系数法转化为方程组解决问题.
(2)分两种情形①当0<t<$\frac{3}{2}$时,P(t,-$\frac{3}{4}$t+$\frac{9}{4}$t+3),②当$\frac{3}{2}$<t<3时,分别求出OM的长即可解决问题.
(3)如图2中,过点C作x轴的平行线,过点B作y轴的平行线,两直线交于点Q,延长MK与CQ交于点N,延长KM与x轴交于点Z,Rt△KBN≌Rt△QBN,推出∠KNB=∠QNB,由NQ∥OB,推出∠QNB=∠NBO=∠KNB,推出ZN=ZB,设EG交CQ于H,由△HNG≌△FGE,推出CH=OE=t=GH,HN=GE=3-t,推出CN=3-t+3=3,推出NQ=BD=1=NK,设ZK=m,则ZB=ZN=m+1,在Rt△KZB中,(m+1)2=m2+32,推出m=4,推出ZB=5,于tan∠GZB=$\frac{3}{4}$,tan∠GEF=$\frac{3}{4}$,可得$\frac{t}{3-t}$=$\frac{3}{4}$,求出t即可解决问题.
解答 解:(1)对于直线y=-x+3,令x=0得y=3,
∴C(0,3),把B(4,0),C(0,3)的坐标代入y=-$\frac{3}{4}$x2+bx+c得$\left\{\begin{array}{l}{-12+4b+c=0}\\{c=3}\end{array}\right.$,解得$\left\{\begin{array}{l}{b=\frac{9}{4}}\\{c=3}\end{array}\right.$,
∴抛物线的解析式为y=-$\frac{3}{4}$x2+$\frac{9}{4}$x+3.
(2)如图1中,当0<t<$\frac{3}{2}$时,P(t,-$\frac{3}{4}$t+$\frac{9}{4}$t+3),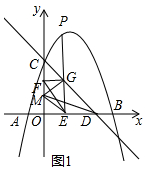
∵FG⊥OC,GE⊥OD,CO⊥OD,
∴四边形FOGE是矩形,
∴OE=FG=t,GE=GD=3-t,
∵MG⊥FE,FG⊥GE,
∴∠GEF+∠GFE=90°,∠GFE+∠FGM=90°,
∴∠GEF=∠FGM,
在Rt△FGE中,tan∠FEG=$\frac{FG}{GE}$=$\frac{t}{3-t}$,
∴在Rt△FGM中,tan∠FGM=$\frac{FM}{GF}$=$\frac{t}{3-t}$,
∴FM=$\frac{{t}^{2}}{3-t}$,
∴OM=FO-FM=(3-t)-$\frac{{t}^{2}}{3-t}$=$\frac{9-6t}{3-t}$,
∴S=$\frac{1}{2}$•DE•OM=$\frac{1}{2}$×(3-t)×$\frac{9-6t}{3-t}$=$\frac{9-6t}{2}$,
当$\frac{3}{2}$<t<3时,S=$\frac{1}{2}$•DE•OM=$\frac{1}{2}$•DE•(FM-OF)=$\frac{-9+6t}{2}$.
综上所述,S=$\left\{\begin{array}{l}{\frac{9-6t}{2}}&{(0<t<\frac{3}{2})}\\{\frac{-9+6t}{2}}&{(\frac{3}{2}<t<3)}\end{array}\right.$.
(3)如图2中,过点C作x轴的平行线,过点B作y轴的平行线,两直线交于点Q,延长MK与CQ交于点N,延长KM与x轴交于点Z,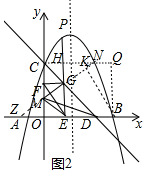
∵CQ∥BO,BQ∥CO,
∴四边形COBQ是平行四边形,
∵∠COB=90°,
∴四边形COBQ是矩形,
∴∠CQB=90°=∠BKN,CO=BQ=3,
对于直线y=-x+3,令y=0得x=3,
∴D(0,3),
∴OD=OC=BQ=3,
∵BK=OD,
∴BK=BQ,∵BN=BN,
∴Rt△KBN≌Rt△QBN,
∴∠KNB=∠QNB,
∵NQ∥OB,
∴∠QNB=∠NBO=∠KNB,
∴ZN=ZB,设EG交CQ于H,
∵OC=OB,
∴∠OCD=∠ODC,
∵CQ∥OB,
∴∠QHG=∠HEO=90°,∠HCD=∠CDO,
∴∠OCD=∠HCD,
∵GF⊥OC,GH⊥CH,
∴GH=GF,
∵GM⊥EF,GH⊥HN,
∴∠GEM+∠MGE=90°,∠HGN+∠HNG=90°,
∵∠HGN=∠MGE,
∴∠GEM=∠HNG,
∵∠GFO=∠FOE=∠OEG=90°,
∴∠GEF=90°=∠GHN,
∴△HNG≌△FGE,
∴CH=OE=t=GH,HN=GE=3-t,
∴CN=3-t+3=3,
∴NQ=BD=1=NK,设ZK=m,则ZB=ZN=m+1,
在Rt△KZB中,(m+1)2=m2+32,
∴m=4,
∴ZB=5,
∴tan∠GZB=$\frac{3}{4}$,tan∠GEF=$\frac{3}{4}$,
∴$\frac{t}{3-t}$=$\frac{3}{4}$,
∴t=$\frac{9}{7}$,
∵抛物线的对称轴x=$\frac{3}{2}$,
∴点P到抛物线的对称轴的距离为$\frac{3}{2}$-$\frac{9}{7}$=$\frac{3}{14}$.
点评 本题考查二次函数综合题、一次函数的应用、待定系数法、矩形的性质和判定、全等三角形的判定和性质、锐角三角函数等知识,解题的关键是学会圆分类讨论的思考思考问题,学会添加常用辅助线,构造全等三角形解决问题,学会用方程的思想解决问题,属于中考压轴题.


科目:初中数学 来源: 题型:选择题
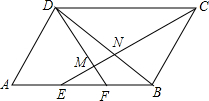 如图,?ABCD中,AE=EF=FB,CE交DF,DB于M,N,则EM:MN:NC=( )
如图,?ABCD中,AE=EF=FB,CE交DF,DB于M,N,则EM:MN:NC=( )| A. | 5:4:12 | B. | 5:3:12 | C. | 4:3:5 | D. | 2:1:4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -0.07205 | B. | -0.03344 | C. | -0.07205 | D. | -0.003344 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
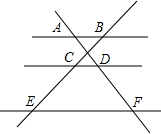 如图,已知AB∥CD∥EF,那么下列结论中正确的是( )
如图,已知AB∥CD∥EF,那么下列结论中正确的是( )| A. | $\frac{CD}{EF}$=$\frac{AD}{AF}$ | B. | $\frac{AB}{CD}$=$\frac{BC}{EC}$ | C. | $\frac{AD}{BC}$=$\frac{AF}{BE}$ | D. | $\frac{CE}{BE}$=$\frac{AF}{AD}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
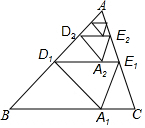 如图,对△ABC纸片进行如下操作:
如图,对△ABC纸片进行如下操作:| A. | $\frac{3}{2}$ | B. | $\frac{7}{4}$ | C. | $\frac{13}{8}$ | D. | $\frac{31}{16}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 若$\sqrt{x-1}$+$\sqrt{1-x}$=y+4,则xy的平方根为1 | B. | 3-2$\sqrt{2}$的绝对值是2$\sqrt{2}$-3 | ||
| C. | 若$\sqrt{{a}^{2}b}$=-a$\sqrt{b}$成立,则a≤0且b≥0 | D. | 若$\sqrt{(1-a)^{2}}$+$\sqrt{(a-3)^{2}}$=2,则a≥3 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
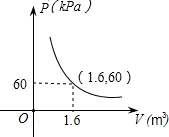 某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压p(单位:kPa)是气体体积V(单位:m3)的反比例函数,其图象如图.当气球内的气压大于120kPa时,气球将爆炸.为了安全起见,气球的体积应( )
某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压p(单位:kPa)是气体体积V(单位:m3)的反比例函数,其图象如图.当气球内的气压大于120kPa时,气球将爆炸.为了安全起见,气球的体积应( )| A. | 不小于$\frac{5}{4}$ m3 | B. | 小于$\frac{5}{4}$ m3 | C. | 不小于$\frac{4}{5}$ m3 | D. | 小于$\frac{4}{5}$ m3 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (3,8) | B. | (3,-8) | C. | (-8,-3) | D. | (-4,-6) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com