
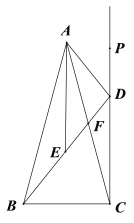
【题目】如图,在△ABC中,AB=AC,点F是AC边上的中点,DC⊥BC,与BF的延长线交于点D,AE平分∠BAC交BF于点E.
(1)求证:AE∥DC;
(2)若BD=8![]() ,求AD的长;
,求AD的长;
(3)若∠BAC=30°,AC=12,点P是射线CD上一点,求![]() CP+AP的最小值.
CP+AP的最小值.
【答案】(1)见解析;(2)4![]() ;(3)6
;(3)6![]()
【解析】
(1)根据等腰三角形的“三线合一”得AN⊥BC,再利用平行线的性质即可证明AE∥CD;
(2)连接CE,由等腰三角形的“三线合一”得出BN=CN,结合AN∥CD和CD⊥BC得到CE=![]() BD,再由AE∥CD和F为AC的中点证明△AEF≌△CDF,进而得到四边形AECD是平行四边形,所以AD=CE即可解答;
BD,再由AE∥CD和F为AC的中点证明△AEF≌△CDF,进而得到四边形AECD是平行四边形,所以AD=CE即可解答;
(3)在∠ACD外作∠DCG=30°,过CD上一点P1作P1M1⊥CG于M1,连接AP1,过点A作AM⊥CG交CD于点P.则P1M1=![]() CP1,PM=
CP1,PM=![]() CP,利用垂线段最短得知AM的长度为所求的最小值,进而在Rt△ACM中求得AM即可.
CP,利用垂线段最短得知AM的长度为所求的最小值,进而在Rt△ACM中求得AM即可.
证明:(1)延长AE交BC于点N.
∵AB=AC,AE平分∠BAC,∴AN⊥BC.
又∵CD⊥BC,
∴AE∥CD
(2)连接CE.
∵AB=AC,AE平分∠BAC,
∴BN=CN.
又∵AN∥CD,
∴BE=ED.
∵∠BCD=90°,
∴CE=![]() BD
BD
∵F是AC中点,
∴AF=CF.
∴AE∥CD.
∴∠EAC=∠DCA,∠AED=∠CDE.
∴△AEF≌△CDF(AAS).
∴EF=DF.
又AF=CF,
∴四边形AECD是平行四边形.
∴AD=CE=![]() BD,
BD,
∵BD=8![]() ,
,
∴AD=4![]()
(3)在∠ACD外作∠DCG=30°.
过CD上一点P1作P1M1⊥CG于M1,连接AP1,过点A作AM⊥CG交CD于点P.
在Rt△CP1M1和Rt△CPM中,∠DCG=30°,则P1M1=![]() CP1,PM=
CP1,PM=![]() CP.
CP.
∴![]() CP1+AP1=P1M1+AP1,
CP1+AP1=P1M1+AP1,![]() CP+AP=PM+AP=AM.
CP+AP=PM+AP=AM.
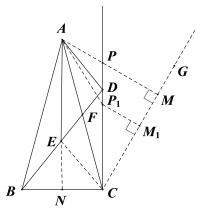
由“垂线段最短”可得P1M1+AP1≥AM,当A、P、M三点共线且AM⊥CM时,![]() CP+AP最小.
CP+AP最小.
∵∠BAC=30°,AE平分∠BAC,
∴∠EAC=15°.
∵AE∥CD,
∴∠DCA=∠EAC=15°.
∴∠ACM=∠ACD+∠DCM=45°.
在等腰Rt△ACM中,AC=12,
由勾股定理得2AM2=AC2=122
∴AM=6![]() .
.
∴![]() CP+AP的最小值是6
CP+AP的最小值是6![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,以Rt△ABC的AC边为直径作⊙O交斜边AB于点E,连接EO并延长交BC的延长线于点D,点F为BC的中点,连接EF和AD.
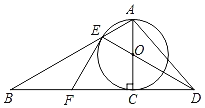
(1)求证:EF是⊙O的切线;
(2)若⊙O的半径为2,∠EAC=60°,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c(a≠0)的顶点为C(2,﹣1),与x轴交于A,B两点,OA=3;

(1)求此抛物线的解析式;
(2)如图1,一次函数y=﹣x+3图象交x轴于点A,交y轴于点D,连结AC、BD,在x轴上有一点Q,使△AQC 与△ABD相似,求出点Q坐标;
(3)如图2,在直线y=kx -1(k>0)上是否存在唯一一点P,使得∠APB=90°?若存在,请直接写出此时k的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一个18米高的楼顶上有一信号塔DC,李明同学为了测量信号塔的高度,在地面的A处测的信号塔下端D的仰角为30°,然后他正对塔的方向前进了18米到达地面的B处,又测得信号塔顶端C的仰角为60°,CD⊥AB与点E,E、B、A在一条直线上.请你帮李明同学计算出信号塔CD的高度(结果保留整数,![]() ≈1.7,
≈1.7,![]() ≈1.4 )
≈1.4 )
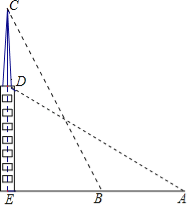
查看答案和解析>>
科目:初中数学 来源: 题型:
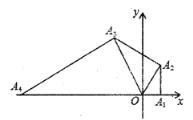
【题目】如图,在平面直角坐标系中,点![]() 的坐标为(1,0),以
的坐标为(1,0),以![]() 为直角边作
为直角边作![]() ,并使
,并使![]() ,再以
,再以![]() 为直角边作
为直角边作![]() ,并使
,并使![]() ,再以
,再以![]() 为直角边作
为直角边作![]() ,并使
,并使![]() ……按此规律进行下去,则点
……按此规律进行下去,则点![]() 的坐标为_________.
的坐标为_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新冠疫情爆发后,各地启动了抗击新冠肺炎的一级应急响应机制,某社区20位90后积极参与社区志愿者工作,充分展示了新时代青年的责任担当,这20位志愿者的年龄统计如表,则他们年龄的众数和中位数分别是( )

A.25岁,25岁B.25岁,26岁C.26岁,25岁D.26岁,26岁
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学准备随机选出七、八、九三个年级各1名学生担任学校国旗升旗手.现已知这三个年级每个年级分别选送一男、一女共6名学生作为备选人.
(1)请你利用树状图或表格列出所有可能的选法;
(2)求选出“一男两女”三名国旗升旗手的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在⊙O中,直径AB垂直弦CD于E,过点A作∠DAF=∠DAB,过点D作AF的垂线,垂足为F,交AB的延长线于点P,连接CO并延长交⊙O于点G,连接EG,已知DE=4,AE=8.
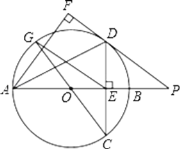
(1)求证:DF是⊙O的切线;
(2)求证:OC2=OEOP;
(3)求线段EG的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com