
【题目】如图,抛物线y=ax2+bx+c(a≠0)的顶点为C(2,﹣1),与x轴交于A,B两点,OA=3;

(1)求此抛物线的解析式;
(2)如图1,一次函数y=﹣x+3图象交x轴于点A,交y轴于点D,连结AC、BD,在x轴上有一点Q,使△AQC 与△ABD相似,求出点Q坐标;
(3)如图2,在直线y=kx -1(k>0)上是否存在唯一一点P,使得∠APB=90°?若存在,请直接写出此时k的值;若不存在,请说明理由.
【答案】(1)y=x2﹣4x+3;(2)Q点的坐标为(0,0)或(![]() ,0);(3)存在,k=1,k=
,0);(3)存在,k=1,k=![]() ,k=
,k=![]() .
.
【解析】
(1)由顶点坐标为C(2,﹣1)可得对称轴为x=2,然后再根据二次函数图像的对称性,确定A、B的坐标,然后使用待定系数法即可解答;
(2)先通过等腰三角形和相似三角形的性质得到∠CAQ=∠DAB=45°,然后分![]() =
=![]() 和
和![]() =
=![]() 两种情况解答即可;
两种情况解答即可;
(3)设P点坐标为(a,ka-1),以AB的中点O为圆心作⊙O,以AB为直径画圆恰好与直线y=kx-1(k>0)相切与P点,然后确定圆的半径长度,然后运用两点间距离公式列方程,最后根据条件即可确定k的取值.
解(1)∵函数图像的顶点坐标为C(2,﹣1)
∴对称轴为x=2
∵OA=3
∴B点的横坐标为:2-(3-2)=1,A点的横坐标为3
∴A(3,0),B(1,0)
∴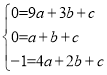 解得
解得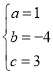
∴函数解析式为y=x2﹣4x+3;
(2)如图:连接AC、QC、BD,
令x=0,则y=﹣0+3=3,即点D坐标为(0,3)
∴OA=OD
∴∠DAB=45°
要使△AQC∽△ADB,则∠CAQ=∠DAB=45°,
①当![]() =
=![]() 时,△AQC∽△ADB,即
时,△AQC∽△ADB,即![]() =
=![]() ,解得AQ=3,此时Q(0,0);
,解得AQ=3,此时Q(0,0);
②当![]() =
=![]() 时,△AQC∽△ABD,即
时,△AQC∽△ABD,即![]() =
=![]() ,解得AQ=
,解得AQ=![]() ,此时Q(
,此时Q(![]() ,0);
,0);
综上所述,Q点的坐标为(0,0)或(![]() ,0);
,0);
(3)连接设P点坐标为(a,ka-1),以AB的中点O为圆心作⊙O,以AB为直径画圆恰好与直线y=kx-1(k>0)相切与P点,即AP⊥BP
∵A(3,0),B(1,0)
∴AO=BO=![]() AB=1
AB=1
∴![]() 即:(k-1)a2-(2k+2)a+1=0
即:(k-1)a2-(2k+2)a+1=0
∵在直线y=kx-1(k>0)上是否存在唯一一点P,使得∠APB=90°
∴①当(k-1)a2-(2k+2)a+1=0为关于a的一元一次方程时,则k-1=1,即k=1;
②①当(k-1)a2-(2k+2)a+1=0为关于a的一元二次方程时,则:
(2k+2)2-4(k-1)=0解得:k=![]() ,k=
,k=![]() ;
;
综上,存在满足题意得k且取值为k=1,k=![]() ,k=
,k=![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
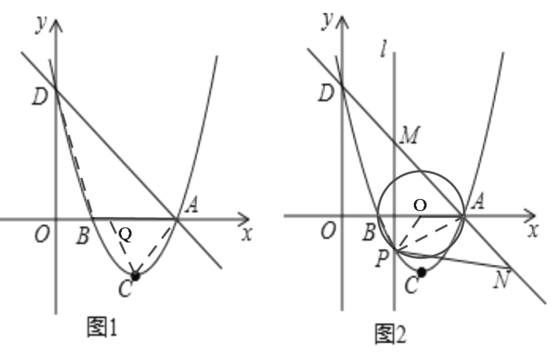
【题目】如图,AB为⊙O的直径,C为⊙O上一点,经过点C的切线交AB的延长线于点E,AD⊥EC交EC的延长线于点D,AD交⊙O于F,FM⊥AB于H,分别交⊙O、AC于M、N,连接MB,BC.
(1)求证:AC平分∠DAE;
(2)若cosM=![]() ,BE=1,①求⊙O的半径;②求FN的长.
,BE=1,①求⊙O的半径;②求FN的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
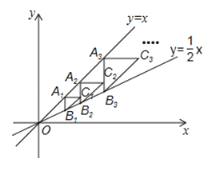
【题目】如图,点A1(2,2)在直线y=x上,过点A1作A1B1∥y轴交直线y=![]() x于点B1,以点A1为直角顶点,A1B1为直角边在A1B1的右侧作等腰直角△A1B1C1,再过点C1作A2B2∥y轴,分别交直线y=x和y=
x于点B1,以点A1为直角顶点,A1B1为直角边在A1B1的右侧作等腰直角△A1B1C1,再过点C1作A2B2∥y轴,分别交直线y=x和y=![]() x于A2,B2两点,以点A2为直角顶点,A2B2为直角边在A2B2的右侧作等腰直角△A2B2C2…,按此规律进行下去,则等腰直角△A8B8C8的面积为_____.
x于A2,B2两点,以点A2为直角顶点,A2B2为直角边在A2B2的右侧作等腰直角△A2B2C2…,按此规律进行下去,则等腰直角△A8B8C8的面积为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
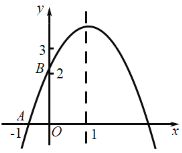
【题目】如图,二次函数![]() 的图象与
的图象与![]() 轴交于
轴交于![]() ,对称轴为直线
,对称轴为直线![]() ,与
,与![]() 轴的交点
轴的交点![]() 在
在![]() 和
和![]() 之间(不包括这两个点),下列结论:①当
之间(不包括这两个点),下列结论:①当![]() 时,
时,![]() ;②
;②![]() ;③当
;③当![]() 时,
时,![]() ;④
;④![]() .其中正确的结论的序号是___________.
.其中正确的结论的序号是___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
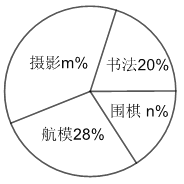
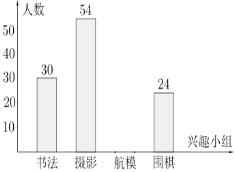
【题目】某校计划组织学生参加“书法”、“摄影”、“航模”、“围棋”四个课外兴题小組.要求每人必须参加.并且只能选择其中一个小组,为了解学生对四个课外兴趣小组的选择情況,学校从全体学生中随机抽取部分学生进行问卷调查,并把调查结果制成如图所示的扇形统计图和条形统计图(部分信息未给出).请你根据给出的信息解答下列问题:
(1)求参加这次问卷调查的学生人数.并补全条形统计图(画图后请标注相应的数据);
(2)![]()
(3)若某校共有1200名学生,试估计该校选择“围棋”课外兴趣小组有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
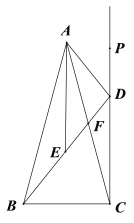
【题目】如图,在△ABC中,AB=AC,点F是AC边上的中点,DC⊥BC,与BF的延长线交于点D,AE平分∠BAC交BF于点E.
(1)求证:AE∥DC;
(2)若BD=8![]() ,求AD的长;
,求AD的长;
(3)若∠BAC=30°,AC=12,点P是射线CD上一点,求![]() CP+AP的最小值.
CP+AP的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
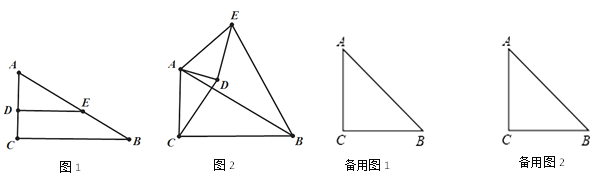
【题目】如图,Rt△ABC中,∠C=90°,E是AB边上一点,D是AC边上一点,且点D不与A、C重合,ED⊥AC.
(1)当sinB=![]() 时,
时,
①求证:BE=2CD.
②当△ADE绕点A旋转到如图2的位置时(45°<∠CAD<90°).BE=2CD是否成立?若成立,请给出证明;若不成立.请说明理由.
(2)当sinB=![]() 时,将△ADE绕点A旋转到∠DEB=90°,若AC=10,AD=2
时,将△ADE绕点A旋转到∠DEB=90°,若AC=10,AD=2![]() ,求线段CD的长.
,求线段CD的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com