
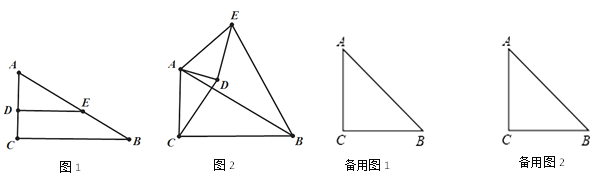
【题目】如图,Rt△ABC中,∠C=90°,E是AB边上一点,D是AC边上一点,且点D不与A、C重合,ED⊥AC.
(1)当sinB=![]() 时,
时,
①求证:BE=2CD.
②当△ADE绕点A旋转到如图2的位置时(45°<∠CAD<90°).BE=2CD是否成立?若成立,请给出证明;若不成立.请说明理由.
(2)当sinB=![]() 时,将△ADE绕点A旋转到∠DEB=90°,若AC=10,AD=2
时,将△ADE绕点A旋转到∠DEB=90°,若AC=10,AD=2![]() ,求线段CD的长.
,求线段CD的长.
【答案】(1)①证明见解析;②BE=2CD成立.理由见解析;(2)2![]() 或4
或4![]() .
.
【解析】
(1)①作EH⊥BC于点H,由sinB=![]() 可得∠B=30°,∠A=60°,根据ED⊥AC可证明四边形CDEH是矩形,根据矩形的性质可得EH=CD,根据正弦的定义即可得BE=2CD;
可得∠B=30°,∠A=60°,根据ED⊥AC可证明四边形CDEH是矩形,根据矩形的性质可得EH=CD,根据正弦的定义即可得BE=2CD;
②根据旋转的性质可得∠BAC=∠EAD,利用角的和差关系可得∠CAD=∠BAE,根据![]() =
=![]() 可证明△ACD∽△ABE,及相似三角形的性质可得
可证明△ACD∽△ABE,及相似三角形的性质可得![]() ,进而可得BE=2CD;
,进而可得BE=2CD;
(2)由sinB=![]() 可得∠ABC=∠BAC=∠DAE=45°,根据ED⊥AC可得AD=DE,AC=BC,如图,分两种情况讨论,通过证明△ACD∽△ABE,求出CD的长即可.
可得∠ABC=∠BAC=∠DAE=45°,根据ED⊥AC可得AD=DE,AC=BC,如图,分两种情况讨论,通过证明△ACD∽△ABE,求出CD的长即可.
(1)①作EH⊥BC于点H,
∵Rt△ABC中,∠C=90°,sinB=![]() ,
,
∴∠B=30°,
∴∠A=60°,
∵ED⊥AC
∴∠ADE=∠C=90°,
∴四边形CDEH是矩形,即EH=CD.
∴在Rt△BEH中,∠B=30°
∴BE=2EH
∴BE=2CD.
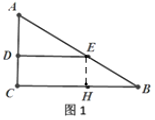
②BE=2CD成立.
理由:∵△ADE绕点A旋转到如图2的位置,
∴∠BAC=∠EAD=60°,
∴∠BAC+∠BAD=∠EAD+∠BAD,即∠CAD=∠BAE,
∵AC:AB=1:2,AD:AE=1:2,
∴![]() ,
,
∴△ACD∽△ABE,
∴![]() ,
,
又∵Rt△ABC中,![]() =2,
=2,
∴![]() =2,即BE=2CD.
=2,即BE=2CD.
(2)∵sinB=![]() ,
,
∴∠ABC=∠BAC=∠DAE=45°,
∵ED⊥AC,
∴∠AED=∠BAC=45°,
∴AD=DE,AC=BC,
将△ADE绕点A旋转,∠DEB=90°,分两种情况:
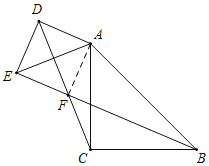
①如图所示,过A作AF⊥BE于F,则∠F=90°,
当∠DEB=90°时,∠ADE=∠DEF=90°,
又∵AD=DE,
∴四边形ADEF是正方形,
∴AD=AF=EF=2![]() ,
,
∵AC=10=BC,
∴AB=10![]() ,
,
∴Rt△ABF中,BF=![]() =6
=6![]() ,
,
∴BE=BF﹣EF=4![]() ,
,
又∵△ABC和△ADE都是直角三角形,
且∠BAC=∠EAD=45°,
∴∠CAD=∠BAE,
∵AC:AB=1:![]() ,AD:AE=1:
,AD:AE=1:![]() ,
,
∴![]() ,
,
∴△ACD∽△ABE,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
∴CD=2![]() ;
;

②如图所示,过A作AF⊥BE于F,则∠AFE=∠AFB=90°,
当∠DEB=90°,∠DEB=∠ADE=90°,
又∵AD=ED,
∴四边形ADEF是正方形,
∴AD=EF=AF=2![]() ,
,
又∵AC=10=BC,
∴AB=10![]() ,
,
∴Rt△ABF中,BF=![]() =6
=6![]() ,
,
∴BE=BF+EF=8![]() ,
,
又∵△ACD∽△ABE,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
∴CD=4![]() ,
,
综上所述,线段CD的长为2![]() 或4
或4![]() .
.


 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c(a≠0)的顶点为C(2,﹣1),与x轴交于A,B两点,OA=3;

(1)求此抛物线的解析式;
(2)如图1,一次函数y=﹣x+3图象交x轴于点A,交y轴于点D,连结AC、BD,在x轴上有一点Q,使△AQC 与△ABD相似,求出点Q坐标;
(3)如图2,在直线y=kx -1(k>0)上是否存在唯一一点P,使得∠APB=90°?若存在,请直接写出此时k的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新冠疫情爆发后,各地启动了抗击新冠肺炎的一级应急响应机制,某社区20位90后积极参与社区志愿者工作,充分展示了新时代青年的责任担当,这20位志愿者的年龄统计如表,则他们年龄的众数和中位数分别是( )

A.25岁,25岁B.25岁,26岁C.26岁,25岁D.26岁,26岁
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学准备随机选出七、八、九三个年级各1名学生担任学校国旗升旗手.现已知这三个年级每个年级分别选送一男、一女共6名学生作为备选人.
(1)请你利用树状图或表格列出所有可能的选法;
(2)求选出“一男两女”三名国旗升旗手的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于一个函数,自变量x取a时,函数值y也等于a,我们称a为这个函数的不动点.如果二次函数y=x2+2x+c有两个相异的不动点x1、x2,且x1<1<x2,则c的取值范围是( )
A. c<﹣3B. c<﹣2C. c<![]() D. c<1
D. c<1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学对本校初2017届500名学生中中考参加体育加试测试情况进行调查,根据男生1000米及女生800米测试成绩整理,绘制成不完整的统计图,(图①,图②),请根据统计图提供的信息,回答下列问题:
(1)该校毕业生中男生有 人;扇形统计图中a= ;

(2)补全条形统计图;
(3)若500名学生中随机抽取一名学生,这名学生该项成绩在8分及8分以下的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】保护环境卫生,垃圾分类开始实施.我市为了促进生活垃圾的分类处理,将生活垃圾分为“可回收物”、“有害垃圾”、“湿垃圾”、“干垃圾”四类,并且设置了相应的垃圾箱.

(1)小亮将妈妈分类好的某类垃圾随机投入到四种垃圾箱某类箱内,请写出小亮投放正确的概率为 ;
(2)经过妈妈的教育,小明已经分清了“有害垃圾”,但仍然分不清“可回收物”、“湿垃圾”和“干垃圾”,这天小亮要将妈妈分类好的四类垃圾投入到四种垃圾箱内,请求出小明投放正确的概率;
(3)请你就小亮投放垃圾的事件提出两条合理化建议.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在⊙O中,直径AB垂直弦CD于E,过点A作∠DAF=∠DAB,过点D作AF的垂线,垂足为F,交AB的延长线于点P,连接CO并延长交⊙O于点G,连接EG,已知DE=4,AE=8.
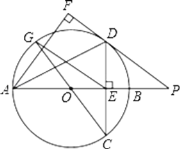
(1)求证:DF是⊙O的切线;
(2)求证:OC2=OEOP;
(3)求线段EG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,顶点为![]() 的抛物线
的抛物线![]() 与交
与交![]() 轴分别于点
轴分别于点![]() ,
,![]() (点
(点![]() 在点
在点![]() 的左侧),与交
的左侧),与交![]() 轴交于点
轴交于点![]() .已知直线
.已知直线![]() 的解析式为
的解析式为![]() .
.
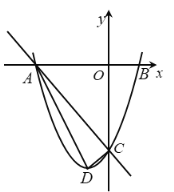
(1)求抛物线的解析式:
(2)若以点![]() 为圆心的圆与
为圆心的圆与![]() 相切,求
相切,求![]() 的半径;
的半径;
(3)在![]() 轴上是否存在一点
轴上是否存在一点![]() ,使得以
,使得以![]() ,
,![]() ,
,![]() 三点为顶点的三角形与
三点为顶点的三角形与![]() 相似?如果存在,请求出点
相似?如果存在,请求出点![]() 的坐标;如果不存在,请说明理由.
的坐标;如果不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com