
【题目】如图,以Rt△ABC的AC边为直径作⊙O交斜边AB于点E,连接EO并延长交BC的延长线于点D,点F为BC的中点,连接EF和AD.
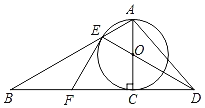
(1)求证:EF是⊙O的切线;
(2)若⊙O的半径为2,∠EAC=60°,求AD的长.
【答案】(1)见解析;(2)AD=![]() .
.
【解析】
(1)连接FO,可根据三角形中位线的性质可判断易证OF∥AB,然后根据直径所对的圆周角是直角,可得CE⊥AE,进而知OF⊥CE,然后根据垂径定理可得∠FEC=∠FCE,∠OEC=∠OCE,再通过Rt△ABC可知∠OEC+∠FEC=90°,因此可证FE为⊙O的切线;
(2)在Rt△OCD中和Rt△ACD中,分别利用勾股定理分别求出CD,AD的长即可 .
(1)证明:连接CE,如图所示:
∵AC为⊙O的直径,
∴∠AEC=90°.
∴∠BEC=90°,
∵点F为BC的中点,
∴EF=BF=CF,
∴∠FEC=∠FCE,
∵OE=OC,
∴∠OEC=∠OCE,
∵∠FCE+∠OCE=∠ACB=90°,
∴∠FEC+∠OEC=∠OEF=90°,
∴EF是⊙O的切线.
(2)解:∵OA=OE,∠EAC=60°,
∴△AOE是等边三角形.
∴∠AOE=60°,
∴∠COD=∠AOE=60°,
∵⊙O的半径为2,
∴OA=OC=2
在Rt△OCD中,∵∠OCD=90°,∠COD=60°,
∴∠ODC=30°,
∴OD=2OC=4,
∴CD=![]() .
.
在Rt△ACD中,∵∠ACD=90°,AC=4,CD=![]() .
.
∴AD=![]() =
=![]() .
.


科目:初中数学 来源: 题型:
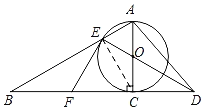
【题目】如图,AB为⊙O的直径,C为⊙O上一点,经过点C的切线交AB的延长线于点E,AD⊥EC交EC的延长线于点D,AD交⊙O于F,FM⊥AB于H,分别交⊙O、AC于M、N,连接MB,BC.
(1)求证:AC平分∠DAE;
(2)若cosM=![]() ,BE=1,①求⊙O的半径;②求FN的长.
,BE=1,①求⊙O的半径;②求FN的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
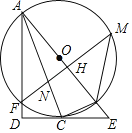
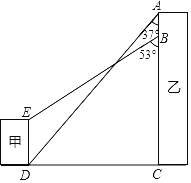
【题目】如图,某地有甲、乙两栋建筑物,小明于乙楼楼顶A点处看甲楼楼底D点处的俯角为37°,走到乙楼B点处看甲楼楼顶E点处的俯角为53°,已知AB=6m,DE=10m.求乙楼的高度AC的长.(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,sin53°≈0.80,cos53°≈0.60,tan53°≈1.33,精确到0.1m)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:
关于三角函数还有如下的公式:
![]()
![]()
利用这些公式可以将一些不是特殊角的三角函数转化为特殊角的三角函数来求值.
例:![]()
=![]()
=![]()
=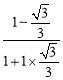
=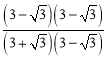
=![]() =
=
![]()
根据以上阅读材料,请选择适当的公式解答下面问题
(1)计算:sin15°;
(2)乌蒙铁塔是六盘水市标志性建筑物之一(图1),小华想用所学知识来测量该铁塔的高度,如图2,小华站在离塔底A距离7米的C处,测得塔顶的仰角为75°,小华的眼睛离地面的距离DC为1.62米,请帮助小华求出乌蒙铁塔的高度.(精确到0.1米,参考数据![]() )
)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,为放置在水平桌面![]() 上的台灯,底座的高
上的台灯,底座的高![]() 为
为![]() .长度均为
.长度均为![]() 的连杆
的连杆![]() ,
,![]() 与
与![]() 始终在同一水平面上.
始终在同一水平面上.
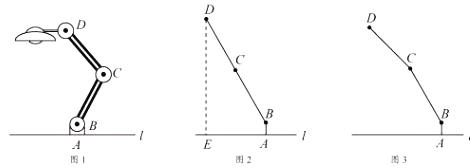
(1)旋转连杆![]() ,
,![]() ,使
,使![]() 成平角,
成平角,![]() ,如图2,求连杆端点
,如图2,求连杆端点![]() 离桌面
离桌面![]() 的高度
的高度![]() .
.
(2)将(1)中的连杆![]() 绕点
绕点![]() 逆时针旋转,使
逆时针旋转,使![]() ,如图3,问此时连杆端点
,如图3,问此时连杆端点![]() 离桌面
离桌面![]() 的高度是增加了还是减少?增加或减少了多少?(精确到
的高度是增加了还是减少?增加或减少了多少?(精确到![]() ,参考数据:
,参考数据:![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
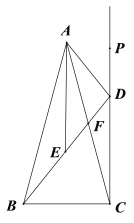
【题目】如图,在△ABC中,AB=AC,点F是AC边上的中点,DC⊥BC,与BF的延长线交于点D,AE平分∠BAC交BF于点E.
(1)求证:AE∥DC;
(2)若BD=8![]() ,求AD的长;
,求AD的长;
(3)若∠BAC=30°,AC=12,点P是射线CD上一点,求![]() CP+AP的最小值.
CP+AP的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com