
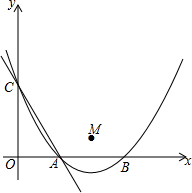
 如图,抛物线y=$\frac{1}{3}$x2-$\frac{4\sqrt{3}}{3}$x+3与x轴交于A,B两点,与y轴交于点C,点M的坐标为(2$\sqrt{3}$,1).以M为圆心,2为半径作⊙M.则下列说法正确的是①②③④(填序号).
如图,抛物线y=$\frac{1}{3}$x2-$\frac{4\sqrt{3}}{3}$x+3与x轴交于A,B两点,与y轴交于点C,点M的坐标为(2$\sqrt{3}$,1).以M为圆心,2为半径作⊙M.则下列说法正确的是①②③④(填序号).分析 过点M作MN⊥AB于点N,交⊙M于点D,则AN=BN,先根据A、B、C的坐标,求出OA、OC、AN,根据tan∠OAC=$\frac{OC}{OA}$=$\sqrt{3}$得出①正确,∠CAO=60°,
再根据tan∠MAN=$\frac{\sqrt{3}}{3}$,得出∠MAN=30°,证出MA⊥AC,得出直线AC是⊙M的切线,②正确,求出D点的坐标为(2$\sqrt{3}$,-1),再根据抛物线的顶点坐标为(2$\sqrt{3}$,-1),得出③正确,根据MA⊥AC,求出CM=4,得出点C到⊙M的最远距离为4+2=6,④正确,根据∠AOC=90°,∠AMC≠90°,得出△AOC与△AMC关于直线AC不对称,⑤错误.
解答 解:过点M作MN⊥AB于点N,交⊙M于点D,
则AN=BN,
∵抛物线y=$\frac{1}{3}$x2-$\frac{4\sqrt{3}}{3}$x+3与x轴交于A,B两点,与y轴交于点C,
∴A,B两点的坐标是($\sqrt{3}$,0),(3$\sqrt{3}$,0),点C的坐标为(0,3),
∴OA=$\sqrt{3}$,OC=3,AN=$\sqrt{3}$,
∴tan∠OAC=$\frac{OC}{OA}$=$\frac{3}{\sqrt{3}}$=$\sqrt{3}$,
∴①正确,∠CAO=60°,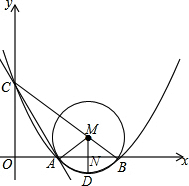
∵点M的坐标为(2$\sqrt{3}$,1),
∴MN=1,
∵tan∠MAN=$\frac{MN}{AN}$=$\frac{1}{\sqrt{3}}$=$\frac{\sqrt{3}}{3}$,
∴∠MAN=30°,
∴MA⊥AC,
∴直线AC是⊙M的切线,
∴②正确,
∵⊙M的半径为2,
∴DN=1,
∴D点的坐标为(2$\sqrt{3}$,-1),
∵抛物线y=$\frac{1}{3}$x2-$\frac{4\sqrt{3}}{3}$x+3的顶点坐标为(2$\sqrt{3}$,-1),
∴⊙M过抛物线的顶点,
∴③正确,
∵OA=$\sqrt{3}$,∠ACO=30°,
∴AC=2$\sqrt{3}$,
∵MA⊥AC,
∴CM=$\sqrt{A{C}^{2}+A{M}^{2}}$=$\sqrt{(2\sqrt{3})^{2}+{2}^{2}}$=4,
∴点C到⊙M的最远距离为4+2=6,
∴④正确,
∵∠AOC=90°,∠AMC≠90°,
∴△AOC与△AMC关于直线AC不对称,
∴⑤错误,
故答案为:①②③④.
点评 此题考查了二次函数综合,用到的知识点是二次函数的图象与性质、勾股定理、切线的判定、垂径定理等,关键是综合运用有关定理对每个命题进行判断.


 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:初中数学 来源: 题型:选择题
| A. | 1.2×103米 | B. | 12×103米 | C. | 1.2×104米 | D. | 1.2×105米 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (x2+y2-4)2 | B. | (x-y)4 | C. | (x2-y2-4)2 | D. | (x2+y2+4)2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com