
【题目】如图,AB是⊙O的直径,且AB=6,C是⊙O上一点,D是 ![]() 的中点,过点D作⊙O的切线,与AB,AC的延长线分别交于点E,F,连接AD.
的中点,过点D作⊙O的切线,与AB,AC的延长线分别交于点E,F,连接AD.
(1)求证:AF⊥EF;
(2)填空:
①当BE=时,点C是AF的中点;
②当BE=时,四边形OBDC是菱形.
【答案】
(1)解:连接OD,BD,BC,
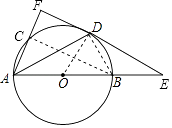
∵ED为⊙O的切线,
∴OD⊥EF,
∵D是 ![]() 的中点,
的中点,
∴OD⊥BC,
∴EF∥BC,
∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠AFE=90°,
∴AF⊥EF;
(2)6,3
【解析】(2)①当BE=6时,
解:由(1)知,BC∥EF,当AB=BE时,AC=CF,
∴当BE=6时,点C是AF的中点,
所以答案是:6;
②当BE=3时,
解:∵AB是⊙O的直径,AB=6,
∴OB=OD=OC=BE=3,
∵ED为⊙O的切线,
∴OD⊥EF,
∴BD=OB=BE,
∵D是 ![]() 的中点,
的中点,
∴CD=BD,
∴CD=BD=BO=OD,
四边形OBDC是菱形.
所以答案是:3.
【考点精析】认真审题,首先需要了解菱形的判定方法(任意一个四边形,四边相等成菱形;四边形的对角线,垂直互分是菱形.已知平行四边形,邻边相等叫菱形;两对角线若垂直,顺理成章为菱形),还要掌握垂径定理的推论(推论1:A、平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧B、弦的垂直平分线经过圆心,并且平分弦所对的两条弧C、平分弦所对的一条弧的直径,垂直平分弦,并且平分弦所对的另一条弧;推论2 :圆的两条平行弦所夹的弧相等)的相关知识才是答题的关键.


 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案科目:初中数学 来源: 题型:
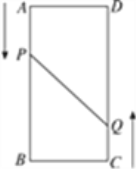
【题目】如图,A,B,C,D为矩形的四个顶点,AB=16 cm,BC=6 cm,动点P,Q分别从点A,C同时出发,点P以3 cm/s的速度向点B移动,点Q以2 cm/s的速度向点D移动.当点P运动到点B停止时,点Q也随之停止运动.问几秒时点P和点Q的距离是10 cm?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,点
,点![]() ,
,![]() 分别是边
分别是边![]() ,
,![]() 上的点,点
上的点,点![]() 是一动点.记
是一动点.记![]() 为
为![]() ,
,![]() 为
为![]() ,
,![]() 为
为![]() .
.
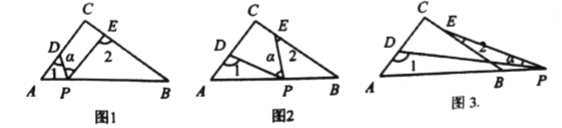
(1)若点![]() 在线段
在线段![]() 上,且
上,且![]() ,如图1,则
,如图1,则![]() _____________;
_____________;
(2)若点![]() 在边
在边![]() 上运动,如图2所示,请猜想
上运动,如图2所示,请猜想![]() ,
,![]() ,
,![]() 之间的关系,并说明理由;
之间的关系,并说明理由;
(3)若点![]() 运动到边
运动到边![]() 的延长线上,如图3所示,则
的延长线上,如图3所示,则![]() ,
,![]() ,
,![]() 之间又有何关系?请直接写出结论,不用说明理由.
之间又有何关系?请直接写出结论,不用说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知平行四边形![]() 中,
中, ![]() ,垂足为
,垂足为![]() 与
与![]() 的延长线相交于
的延长线相交于![]() ,且
,且![]() ,连接
,连接![]() ;
;
(1)如图![]() ,求证:四边形
,求证:四边形![]() 是菱形;
是菱形;
(2)如图![]() ,连接
,连接![]() ,若
,若![]() ,在不添加任何辅助线的情况下,直接写出图
,在不添加任何辅助线的情况下,直接写出图![]() 中所有面积等于
中所有面积等于![]() 的面积的钝角三角形.
的面积的钝角三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某校九年级学生的身高情况,随机抽取部分学生的身高进行调查,利用所得数据绘成如图统计图表:
频数分布表
身高分组 | 频数 | 百分比 |
x<155 | 5 | 10% |
155≤x<160 | a | 20% |
160≤x<165 | 15 | 30% |
165≤x<170 | 14 | b |
x≥170 | 6 | 12% |
总计 | 100% |
(1)填空:a=____,b=____;
(2)补全频数分布直方图;
(3)该校九年级共有600名学生,估计身高不低于165cm的学生大约有多少人?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线y=2x与反比例函数y= ![]() 在第一象限内的图象交于点A(m,2),将直线y=2x向下平移后与反比例函数y=
在第一象限内的图象交于点A(m,2),将直线y=2x向下平移后与反比例函数y= ![]() 在第一象限内的图象交于点P,且△POA的面积为2.
在第一象限内的图象交于点P,且△POA的面积为2.
(1)求k的值.
(2)求平移后的直线的函数解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合题
(1)操作发现:
如图①,在正方形ABCD中,过A点有直线AP,点B关于AP的对称点为E,连接DE交AP于点F,当∠BAP=20°时,则∠AFD=°;当∠BAP=α°(0<α<45°)时,则∠AFD=;猜想线段DF,EF,AF之间的数量关系:DF﹣EF=AF(填系数);
(2)数学思考:
如图②,若将“正方形ABCD中”改成“菱形ABCD中,∠BAD=120°”,其他条件不变,则∠AFD=;线段DF,EF,AF之间的数量关系是否发生改变,若发生改变,请写出数量关系并说明理由;
(3)类比探究:
如图③,若将“正方形ABCD中”改成“菱形ABCD中,∠BAD=α°”,其他条件不变,则∠AFD=°;请直接写出线段DF,EF,AF之间的数量关系: .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=6,BC=4,过对角线BD中点O的直线分别交AB,CD边于点E,F.
(1)求证:四边形BEDF是平行四边形;
(2)当四边形BEDF是菱形时,求EF的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com