
【题目】如图,AB∥CD,分别探讨下面四个图形中∠APC与∠PAB、∠PCD的关系,请你从所得到的关系中任选一个加以说明。(适当添加辅助线,其实并不难)

【答案】(1)∠APC=∠PAB+∠PCD;
(2)∠APC+∠PAB+∠PCD=360°;
(3)∠APC=∠PAB-∠PCD;
(4)∠APC=∠PCD-∠PAB
证明见解析
【解析】
关键过转折点作出平行线,根据两直线平行,内错角相等,或结合三角形的外角性质求证即可.
如图: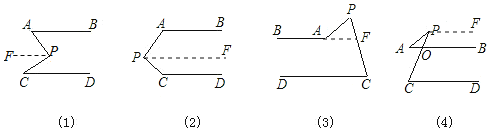
(1)∠APC=∠PAB+∠PCD;
证明:过点P作PF∥AB,则AB∥CD∥PF,
∴∠APC=∠PAB+∠PCD(两直线平行,内错角相等).
(2)∠APC+∠PAB+∠PCD=360°;
(3)∠APC=∠PAB-∠PCD;
(4)∠APC=∠PCD-∠PAB
证明第(4)个结论:
∵AB∥CD,
∴∠POB=∠PCD,
∵∠POB是△AOP的外角,
∴∠APC+∠PAB=∠POB,
∴∠APC=∠POB-∠PAB,
∴∠APC=∠PCD-∠PAB.


科目:初中数学 来源: 题型:
【题目】用5个相同的正方体搭出如图所示的组合体.
(1)分别画出从正面、左面、上面看这个组合体时看到的图形;
(2)如果在这个组合体中,再添加一个相同的正方体组成一个新组合体,从正面、左面看这个新组合体时,看到的图形与原来相同.你认为这个设想能实现吗?若能,画出添加正方体后,从上面看这个组合体时看到的图形;若不能,说明理由.
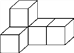
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们给出如下定义:把对角线互相垂直的四边形叫做“正交四边形”.
如图1,在四边形![]() 中,
中,![]() ,四边形
,四边形![]() 就是“正交四边形”.
就是“正交四边形”.
(1)下列四边形,一定是“正交四边形”的是______.
①平行四边形②矩形③菱形④正方形
(2)如图2,在“正交四边形”![]() 中,点
中,点![]() 分别是边
分别是边![]() 的中点,求证:四边形
的中点,求证:四边形![]() 是矩形.
是矩形.
(3)小明说:“计算‘正交四边形’的面积可以仿照菱形的方法,面积是对角线之积的一半.”小明的说法正确吗?如果正确,请给出证明;如果错误,请给出反例.
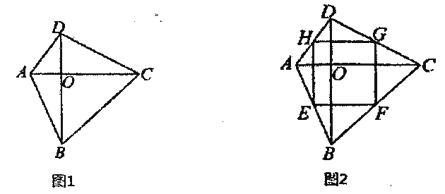
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究题.
用棋子摆成的“T”字形图如图所示:

(1)填写表:
图形序号 | ① | ② | ③ | ④ | … | ⑩ |
每个图案中棋子个数 | 5 | 8 | … |
(2)写出第n个“T”字形图案中棋子的个数(用含n的代数式表示);
(3)第20个“T”字形图案共有棋子多少个?
(4)计算前20个“T”字形图案中棋子的总个数.(提示:请你先思考下列问题:第1个图案与第20个图案中共有多少个棋子?第2个图案与第19个图案中共有多少个棋子?第3个图案与第18个图案呢?)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】微信运动是由腾讯开发的一个类似计步数据库的公众账号,用户可以通过关注微信运动公众号查看自己每天行走的步数,同时也可以和其他用户进行运动量的![]() 或点赞.甲、乙两人开启了微信运动,沿湖边环形道上匀速跑步,已知乙的步距比甲的步距少
或点赞.甲、乙两人开启了微信运动,沿湖边环形道上匀速跑步,已知乙的步距比甲的步距少![]() (步距是指每一步的距离),两人各跑了
(步距是指每一步的距离),两人各跑了![]() 圈,跑
圈,跑![]() 圈前后的时刻和步数如下:
圈前后的时刻和步数如下:
出发时刻 | 出发时微信运动中显示的步数 | 结束时刻 | 结束时微信运动中显示的步数 | |
甲 |
|
|
|
|
乙 |
|
|
|
|
(1)求甲、乙的步距和环形道的周长;
(2)若每![]() 分钟甲比乙多跑
分钟甲比乙多跑![]() 步,求表中
步,求表中![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,甲、乙、丙、丁四位同学给出了四种表示该长方形面积的多项式:
①(2a+b)(m+n);②2a(m+n)+b(m+n);③m(2a+b)+n(2a+b);④2am+2an+bm+bn,你认为其中正确的有( )

A. ①② B. ③④ C. ①②③ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】等腰Rt△ABC和⊙O如图放置,已知AB=BC=1,∠ABC=90°,⊙O的半径为1,圆心O与直线AB的距离为5.
(1)若△ABC以每秒2个单位的速度向右移动,⊙O不动,则经过多少时间△ABC的边与圆第一次相切?
(2)若两个图形同时向右移动,△ABC的速度为每秒2个单位,⊙O的速度为每秒1个单位,则经过多少时间△ABC的边与圆第一次相切?
(3)若两个图形同时向右移动,△ABC的速度为每秒2个单位,⊙O的速度为每秒1个单位,同时△ABC的边长AB、BC都以每秒0.5个单位沿BA、BC方向增大.△ABC的边与圆第一次相切时,点B运动了多少距离?

查看答案和解析>>
科目:初中数学 来源: 题型:
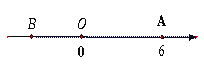
【题目】如图,已知数轴上的点A对应的数为6,B是数轴上的一点,且AB=10,动点P从点A出发,以每秒6个单位长度的速度沿着数轴向左匀速运动,设运动时间为t秒(t>0).
(1)数轴上点B对应的数是_______,点P对应的数是_______(用t的式子表示);
(2)动点Q从点B与点P同时出发,以每秒4个单位长度的速度沿着数轴向左匀速运动,试问:运动多少时间点P可以追上点Q?
(3)M是AP的中点,N是PB的中点,点P在运动过程中,线段MN的长度是否发生变化?若有变化,说明理由;若没有变化,请你画出图形,并求出MN的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com