
【题目】如图,四边形ABCD内接于⊙O,四边形ABCO是平行四边形,则∠1+∠2= ( )

A.45°B.50°C.60°D.75°
科目:初中数学 来源: 题型:
【题目】某水果连锁店销售某种热带水果,其进价为20元/千克.销售一段时间后发现:该水果的日销量![]() (千克)与售价
(千克)与售价![]() (元/千克)的函数关系如图所示:
(元/千克)的函数关系如图所示:
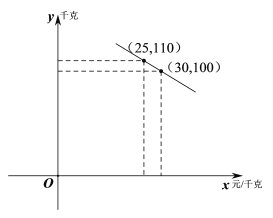
(1)求![]() 关于
关于![]() 的函数解析式;
的函数解析式;
(2)当售价为多少元/千克时,当日销售利润最大,最大利润为多少元?
(3)由于某种原因,该水果进价提高了![]() 元/千克(
元/千克(![]() ),物价局规定该水果的售价不得超过40元/千克,该连锁店在今后的销售中,日销售量与售价仍然满足(1)中的函数关系.若日销售最大利润是
),物价局规定该水果的售价不得超过40元/千克,该连锁店在今后的销售中,日销售量与售价仍然满足(1)中的函数关系.若日销售最大利润是![]() 元,请直接写出
元,请直接写出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,∠ABC=30°,△CDE是等边三角形,点D在边AB上.

(1)如图1,当点E在边BC上时,求证DE=EB;
(2)如图2,当点E在△ABC内部时,猜想ED和EB数量关系,并加以证明;
(3)如图3,当点E在△ABC外部时,EH⊥AB于点H,过点E作GE∥AB,交线段AC的延长线于点G,AG=5CG,BH=3.求CG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某青春党支部在精准扶贫活动中,给结对帮扶的贫困家庭赠送甲、乙两种树苗让其栽种.已知乙种树苗的价格比甲种树苗贵10元,用480元购买乙种树苗的棵数恰好与用360元购买甲种树苗的棵数相同.
(1)求甲、乙两种树苗每棵的价格各是多少元?
(2)在实际帮扶中,他们决定再次购买甲、乙两种树苗共50棵,此时,甲种树苗的售价比第一次购买时降低了10%,乙种树苗的售价不变,如果再次购买两种树苗的总费用不超过1500元,那么他们最多可购买多少棵乙种树苗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在小正方形边长均为1的方格纸中有线段AB,点A、B均在小正方形的顶点上.

(1)以AB为一边画Rt△ABC(点C在小正方形的顶点上),使△ABC的周长为![]() +5;
+5;
(2)在(1)的条件下,以AB为一边作△ABD,(点D在小正方形的顶点上),使![]() ,且△ABD的面积为2;连接CD,并直接写出∠ADC的正切值.
,且△ABD的面积为2;连接CD,并直接写出∠ADC的正切值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】大数学家欧拉非常推崇观察能力,他说过,今天已知的许多数的性质,大部分是通过观察发现的,历史上许多大家,都是天才的观察家,化归就是将面临的新问题转化为已经熟悉的规范问题的数学方法,这是一种具有普遍适用性的数学思想方法.如多项式除以多项式可以类比于多位数的除法进行计算:
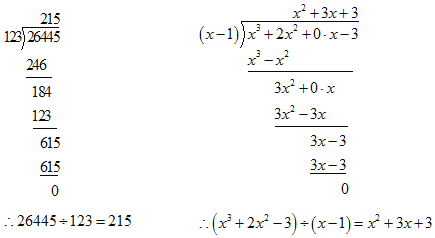
请用以上方法解决下列问题:
(1)计算:(x3+2x2﹣3x﹣10)÷(x﹣2);
(2)若关于x的多项式2x4+5x3+ax2+b能被二项式x+2整除,且a,b均为自然数,求满足以上条件的a,b的值及相应的商.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形纸片ABCD中,点E是AD的中点,且AE=1,连接BE,分别以B、E为圆心,以大于![]() 的长为半径作弧,两弧交于点M、N,若直线MN恰好过点C,则AB的长度为( )
的长为半径作弧,两弧交于点M、N,若直线MN恰好过点C,则AB的长度为( )
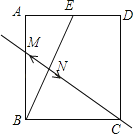
A.![]() B.
B.![]() C.
C.![]() D.2
D.2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com