
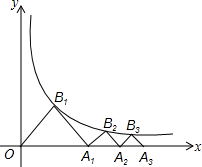
 已知反比例函数$y=\frac{4}{x}$,作等腰Rt△OA1B1,使点B1在反例函数的图象上,点A1在x轴上,再作等腰Rt△A1B2A2,使点B2在反比例函数的图象上,点A2在x轴上;…,再作等腰Rt△A8B9A9,则OA9=12.
已知反比例函数$y=\frac{4}{x}$,作等腰Rt△OA1B1,使点B1在反例函数的图象上,点A1在x轴上,再作等腰Rt△A1B2A2,使点B2在反比例函数的图象上,点A2在x轴上;…,再作等腰Rt△A8B9A9,则OA9=12. 分析 先求得OA1=4,然后根据反比例函数图象上点的坐标特征以及等腰直角三角形的性质求得OA2=4$\sqrt{2}$,0A3=4$\sqrt{3}$,…得出规律,即可求得OA9的值.
解答 解:∵反比例函数$y=\frac{4}{x}$,作等腰Rt△OA1B1,
∴B1(2,2),
∴OA1=4,
设Bn的纵坐标为yn,
根据等腰直角三角形的性质:B2(4+y2,y2),
∴y2(y2+4)=4,
解得y2=2$\sqrt{2}$-2,
∴OA2=4+2(2$\sqrt{2}$-2)=4$\sqrt{2}$,
B3(4$\sqrt{2}$+y3,y3),
∴y3(4$\sqrt{2}$+y3)=4,
解得y3=2$\sqrt{3}$-2$\sqrt{2}$,
∴OA3=4$\sqrt{2}$+2(2$\sqrt{3}$-2$\sqrt{2}$)=4$\sqrt{3}$,
B4(4$\sqrt{3}$+y4,y4),
∴y4(4$\sqrt{3}$+y4)=4,
解得y4=4-2$\sqrt{3}$,
∴OA4=4$\sqrt{3}$+2(4-2$\sqrt{3}$)=8=4$\sqrt{4}$,
…
OAn=4$\sqrt{n}$,
∴OA9=4$\sqrt{9}$=12,.
故答案为12.
点评 本题考查了反比例函数图象上点的坐标特征以及等腰直角三角形的性质,表示出Bn的坐标是解题的关键.


科目:初中数学 来源: 题型:解答题
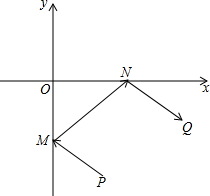 牧马人某天要从马厩牵出马,先到草地边的某一处牧马,再到河边饮水,然后回到帐篷,为了便于研究,以河边为x轴、草地边为y轴建立平面直角坐标系,如图所示,马厩P的坐标为(2,-4),帐篷Q的坐标为(6,-2),请你帮他确定这一天的最短路线.
牧马人某天要从马厩牵出马,先到草地边的某一处牧马,再到河边饮水,然后回到帐篷,为了便于研究,以河边为x轴、草地边为y轴建立平面直角坐标系,如图所示,马厩P的坐标为(2,-4),帐篷Q的坐标为(6,-2),请你帮他确定这一天的最短路线.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
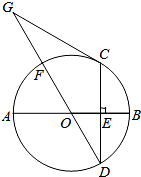 如图,AB是⊙O的直径,CD是弦,CD⊥AB于点E,点G在直径DF的延长线上,∠D=∠G=30°
如图,AB是⊙O的直径,CD是弦,CD⊥AB于点E,点G在直径DF的延长线上,∠D=∠G=30°查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
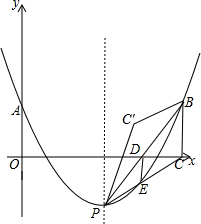 如图,抛物线y=a(x-$\sqrt{2}$m)2-m(其中m>1)与其对称轴l相交于点P,与y轴相交于点A(0,m).点A关于直线l的对称点为B,作BC⊥x轴于点C,连接PC、PB,与抛物线、x轴分别相交于点D、E,连接DE.将△PBC沿直线PB翻折,得到△PBC′.
如图,抛物线y=a(x-$\sqrt{2}$m)2-m(其中m>1)与其对称轴l相交于点P,与y轴相交于点A(0,m).点A关于直线l的对称点为B,作BC⊥x轴于点C,连接PC、PB,与抛物线、x轴分别相交于点D、E,连接DE.将△PBC沿直线PB翻折,得到△PBC′.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ①② | B. | ①②③ | C. | ①②④ | D. | ① |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com