
【题目】昆明某家电专卖店销售每台进价分别200元、160元的A,B两种型号的电风扇,下表是近两周的销售情况

(注:进价、售价均保持不变,利销=销售收入进货成本)
(1)求A,B两种型号的电风扇的销售单价;
(2)若专卖店准备用不多于3560元的金额再采购这两种型号的电风扇共20台,且采购A型电风扇的数量不少于8台.求专卖店有哪几种采购方案?
(3)在(2)的条件下.如果采购的电风扇都能销售完,请直接写出哪种采购方案专卖店所获利润最大?最大利润是多少?
【答案】(1)250元、200元;(2)方案一:购买A种型号的电风扇8台,则B种型号的电风扇12台;方案二:购买A种型号的电风扇9台,则B种型号的电风扇11台;(3)购买A种型号的电风扇9台,则B种型号的电风扇11台获得利润最大,最大利润为890元.
【解析】
(1)根据表格可以列出相应的方程组,从而可以解答本题;
(2)根据题意可以得到相应的不等式组,从而可以求得有几种采购方案;
(3)根据(2)中的购买方案计算出两种方案的利润,然后再进行比较即可.
(1)设A、B两种型号电风扇的销售单价分别为x元、y元,
![]() ,
,
解得:
![]() ,
,
答:A、B两种型号电风扇的销售单价分别为250元、200元;
(2)设购买A种型号的电风扇m台,则B种型号的电风扇(20-m)台,则
![]()
解得,8≤m≤9,
故A、B两种型号的电风扇的采购方案有二种,
方案一:购买A种型号的电风扇8台,则B种型号的电风扇12台;
方案二:购买A种型号的电风扇9台,则B种型号的电风扇11台.
(3)方案一获得的利润为:8×(250-200)+12×(200-160)=880(元),
方案二:获得的利润为:9×(250-200)+11×(200-160)=890(元).
所以,购买A种型号的电风扇9台,则B种型号的电风扇11台获得利润最大,最大利润为890元.


科目:初中数学 来源: 题型:
【题目】为了编撰祖国的优秀传统文化,某校组织了一次“诗词大会”,小明和小丽同时参加,其中,有一道必答题是:从如图所示的九宫格中选取七个字组成一句唐诗,其答案为“山重水复疑无路”.
(1)小明回答该问题时,对第二个字是选“重”还是选“穷”难以抉择,若随机选择其中一个,则小明回答正确的概率是 ;
(2)小丽回答该问题时,对第二个字是选“重”还是选“穷”、第四个字是选“富”还是选“复”都难以抉择,若分别随机选择,请用列表或画树状图的方法求小丽回答正确的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠A=20°,∠ABC与∠ACB的角平分线交于D1,∠ABD1与∠ACD1的角平分线交于点D2,依此类推,∠ABD4与∠ACD4的角平分线交于点D5,则∠BD5C的度数是_____.
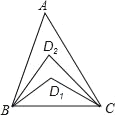
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次800米的长跑比赛中,甲、乙两人所跑的路程![]() (米)与各自所用时间
(米)与各自所用时间![]() (秒)之间的函数图象分别为线段
(秒)之间的函数图象分别为线段![]() 和折线
和折线![]() (如图所示),请根据图象,回答下列问题.
(如图所示),请根据图象,回答下列问题.
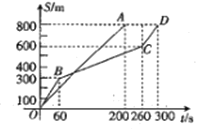
(1)在起跑后60秒时,乙在甲的前面还是后面?
(2)在起跑后多少秒时,两人相遇?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,O为原点,B(0,6),A(8,0),以点B为旋转中心把△ABO逆时针旋转,得△A′BO′,点O,A旋转后的对应点为O′,A′,记旋转角为β.
(1)如图1,若β=90°,求AA′的长;
(2)如图2,若β=120°,求点O′的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB∥CD,∠E=90°,那么∠B+∠D等于多少度?为什么?

解:过点E作EF∥AB,
得∠B+∠BEF=180°(________________________),
因为AB∥CD(已知),
EF∥AB(所作),
所以EF//CD(________________________).
得________________________(两直线平行,同旁内角互补),
所以∠B+∠BEF+∠DEF+∠D=________°(__________).
即∠B+∠BED+∠D=___________°.
因为∠BED=90°(已知),
所以∠B+∠D=___________°(等式性质)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,每个小正方形的边长为1个单位,每个小方格的顶点叫格点.
(1)画出△ABC的AB边上的中线CD;
(2)画出△ABC向右平移4个单位后得到的△A1B1C1;
(3)图中AC与A1C1的关系是: ;
(4)能使S △ABQ=S △ABC的格点Q,共有 个,在图中分别用Q 1,Q 2,…表示出来.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,以BC为直径的⊙O交AB于点D,DE交AC于点E,且∠A=∠ADE.
(1)求证:DE是⊙O的切线;
(2)若AD=16,DE=10,求BC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图在平面直角坐标系xOy中,直线l经过点A(-1,0),点A1,A2,A3,A4,A5,……按所示的规律排列在直线l上.若直线 l上任意相邻两个点的横坐标都相差1、纵坐标也都相差1,若点An(n为正整数)的横坐标为2015,则n= .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com