
【题目】如图,菱形ABCD中,AB=2,∠BAD=60°,E是AB的中点,P是对角线AC上的一个动点,则PE+PB的最小值是( ).
A.1
B.2
C.![]()
D.![]()
【答案】D
【解析】解:如图所示,作E点关于AC对称点E′点,连接E′B,E′B与AC的交点即是P点,
∵菱形ABCD中,AB=2,∠BAD=60°,E是AB的中点,
∴AE′=AE=BE=1,
∴△AEE′为等边三角形,
∴∠AEE′=60°,
∴∠E′EB=120°,
∵BE=EE′,
∴∠EE′B=30°,
∴∠AE′B=90°,
BE′= ![]() ,
,
∵PE+PB=BE′,
∴PE+PB的最小值是: ![]() .
.
故答案为: ![]() .作E点关于AC对称点E′点,连接E′B,E′B与AC的交点即是P点,由菱形性质和题意可得AE′=AE=BE=1,根据等边三角形判定即可知△AEE′为等边三角形,由等边三角形性质可得∠AEE′=60°,由邻补角定义得∠E′EB=120°,根据等腰三角形性质和三角形内角和得∠AE′B=90°,根据勾股定理即可得
.作E点关于AC对称点E′点,连接E′B,E′B与AC的交点即是P点,由菱形性质和题意可得AE′=AE=BE=1,根据等边三角形判定即可知△AEE′为等边三角形,由等边三角形性质可得∠AEE′=60°,由邻补角定义得∠E′EB=120°,根据等腰三角形性质和三角形内角和得∠AE′B=90°,根据勾股定理即可得
BE′=![]() ,由PE+PB=BE′即可得出答案.
,由PE+PB=BE′即可得出答案.


 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,O为原点,点A(0,8),点B(m,0),且m>0.把△AOB绕点A逆时针旋转90°,得△ACD,点O,B旋转后的对应点为C,D,
(1)点C的坐标为 ;
(2)①设△BCD的面积为S,用含m的式子表示S,并写出m的取值范围;
②当S=6时,求点B的坐标(直接写出结果即可).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,已知线段AB、CD相交于点O,连接AC、BD,我们把形如图①的图形称之为“8字形”.
(1)如图①,若∠A=∠D,判断∠C与∠B的数量关系,并说明理由;
(2)如图②,∠CAB和∠BDC的平分线AP和DP相交于点P,并且与CD、AB分别相交于M、N,试解答下列问题:
①仔细观察,在图②中有 个“8字形”;
②∠B=80°,∠C=100°,求∠P的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,排球运动员站在点O处练习发球,将球从D点正上方2m的A处发出,把球看成点,其运行的高度y(m)与运行的水平距离x(m)满足关系式y=a(x﹣k)2+h.已知球与D点的水平距离为6m时,达到最高2.6m,球网与D点的水平距离为9m.高度为2.43m,球场的边界距O点的水平距离为18m,则下列判断正确的是( )
A.球不会过网
B.球会过球网但不会出界
C.球会过球网并会出界
D.无法确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,点 E 在正方形 ABCD 的 AB 边上(不与点 A,B 重合),BD 是对角线,延长 AB 到点 F,使 BF=AE,过点 E 作 BD 的垂线,垂足为 M,连接 AM,CF.
(1)求证:MB=ME;
(2)①用等式表示线段 AM 与 CF 的数量关系,并证明;
②用等式表示线段 AM,BM,DM 之间的数量关系,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,点H是BC的中点,作射线AH,在线段AH及其延长线上分别取点E,F,连结BE,CF.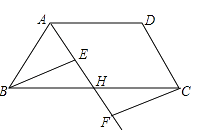
(1)请你添加一个条件,使得△BEH≌△CFH,你添加的条件是,并证明.
(2)在问题(1)中,当BH与EH满足什么关系时,四边形BFCE是矩形,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的盒子中装有颜色不同的8个小球,其中红球3个,黑球5个.
(1)先从袋中取出m(m>1)个红球,再从袋中随机摸出1个球,将“摸出黑球”记为事件A.请完成下列表格:
事件A | 必然事件 | 随机事件 |
m的值 |
(2)先从袋中取出m个红球,再放入m个一样的黑球并摇匀,随机摸出1个球是黑球的概率是![]() ,求m的值.
,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义一种对正整数n的“F”运算:①当n为奇数时,F(n)=3n+1;②当n为偶数时,F(n)=![]() (其中k是使F(n)为奇数的正整数)……,两种运算交替重复进行,例如,取n=24,则:
(其中k是使F(n)为奇数的正整数)……,两种运算交替重复进行,例如,取n=24,则:
![]()
若n=13,则第2018次“F”运算的结果是( )
A. 1 B. 4 C. 2018 D. 42018
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下列填空.
如图,已知∠B+∠BCD=180°,∠B=∠D.求证:∠E=∠DFE.

证明:∵∠B+∠BCD=180°(已知),
∴AB∥CD( ).
∴∠B=∠DCE( ).
又∵∠B=∠D(已知 ),
∴___________ ( 等量代换 ).
∴AD∥BE(内错角相等,两直线平行)
∴∠E=∠DFE( ).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com