
【题目】如图,在平面直角坐标系中,O为原点,点A(0,8),点B(m,0),且m>0.把△AOB绕点A逆时针旋转90°,得△ACD,点O,B旋转后的对应点为C,D,
(1)点C的坐标为 ;
(2)①设△BCD的面积为S,用含m的式子表示S,并写出m的取值范围;
②当S=6时,求点B的坐标(直接写出结果即可).

【答案】(1)C(8,8);(2)①S=0.5m2﹣4m(m>8),或S=﹣0.5m2+4m(0<m<8);②点B的坐标为(4+2![]() ,0)或(2,0)或(6,0).
,0)或(2,0)或(6,0).
【解析】
(1)由旋转的性质得出AC=AO=8,∠OAC=90°,得出C(8,8)即可;
(2)①由旋转的性质得出DC=OB=m,∠ACD=∠AOB=90°,∠OAC=90°,得出∠ACE=90°,证出四边形OACE是矩形,得出DE⊥x轴,OE=AC=8,分三种情况:
a、当点B在线段OE的延长线上时,得出BE=OBOE=m8,由三角形的面积公式得出S=0.5m24m(m>8)即可;
b、当点B在线段OE上(点B不与O,E重合)时,BE=OEOB=8m,由三角形的面积公式得出S=0.5m2+4m(0<m<8)即可;
c、当点B与E重合时,即m=8,△BCD不存在;
②当S=6,m>8时,得出0.5m24m=6,解方程求出m即可;
当S=6,0<m<8时,得出0.5m2+4m=6,解方程求出m即可.
(1)∵点A(0,8),∴AO=8,
∵△AOB绕点A逆时针旋转90°得△ACD,∴AC=AO=8,∠OAC=90°,∴C(8,8),
故答案为(8,8);
(2)①延长DC交x轴于点E,∵点B(m,0),∴OB=m,
∵△AOB绕点A逆时针旋转90°得△ACD,
∴DC=OB=m,∠ACD=∠AOB=90°,∠OAC=90°,∴∠ACE=90°,
∴四边形OACE是矩形,∴DE⊥x轴,OE=AC=8,
分三种情况:
a、当点B在线段OE的延长线上时,如图1所示:
则BE=OB﹣OE=m﹣8,∴S=0.5DCBE=0.5m(m﹣8),即S=0.5m2﹣4m(m>8);
b、当点B在线段OE上(点B不与O,E重合)时,如图2所示:
则BE=OE﹣OB=8﹣m,∴S=0.5DCBE=0.5m(8﹣m),即S=﹣0.5m2+4m(0<m<8);
c、当点B与E重合时,即m=8,△BCD不存在;
综上所述,S=0.5m2﹣4m(m>8),或S=﹣0.5m2+4m(0<m<8);
②当S=6,m>8时,0.5m2﹣4m=6,解得:m=4±2![]() (负值舍去),∴m=4+2
(负值舍去),∴m=4+2![]() ;
;
当S=6,0<m<8时,﹣0.5m2+4m=6,解得:m=2或m=6,
∴点B的坐标为(4+2![]() ,0)或(2,0)或(6,0).
,0)或(2,0)或(6,0).



科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点D是BC边上的一点,∠B=50°,∠BAD=30°,将△ABD沿AD折叠得到△AED,AE与BC交于点F.
(1)填空:∠AFC=______度;
(2)求∠EDF的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校开展以“倡导绿色出行,关爱师生健康”为主题的教育活动.为了了解本校师生的出行方式,在本校范围内随机抽查了部分师生,已知随机抽查的教师人数为学生人数的一半,将收集的数据绘制成下列不完整的两种统计图.

(1)本次共调查了多少名学生?
(2)求学生步行所在扇形的圆心角度数.
(3)求教师乘私家车出行的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,菱形ABCD的顶点A,B的坐标分别为(﹣6,0),(4,0),点D在y轴上.

(1)求点C的坐标;
(2)求对角线AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,∠ABC=90°,AC=AD,M,N分别为AC,CD的中点,连结BM,MN.

(1)求证BM=MN;
(2)若∠BCN=135°,求∠BMN的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,G为CD边中点,连接AG并延长,分别交对角线BD于点F,交BC边延长线于点E.若FG=2,则AE的长度为( )
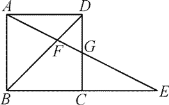
A. 6B. 8
C. 10D. 12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB=DC,AD=BC,E,F在DB上两点且BF=DE,若∠AEB=120°,∠ADB=30°,则∠BCF= ( )

A. 150° B. 40° C. 80° D. 90°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,∠ABC=90°,AB=4cm,BC=8cm,E、F是AD,DC的中点,连接EF、BE、BF,已知四边形ABCD的面积为36![]() ,△DEF的面积是△DAC面积的
,△DEF的面积是△DAC面积的![]() ,求△BEF的面积_____
,求△BEF的面积_____![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD中,AB=2,∠BAD=60°,E是AB的中点,P是对角线AC上的一个动点,则PE+PB的最小值是( ).
A.1
B.2
C.![]()
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com