
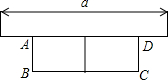
 如图,有长为24米的篱笆,一边利用墙(墙的最大可用长度为3米),当花圃的宽AB为
如图,有长为24米的篱笆,一边利用墙(墙的最大可用长度为3米),当花圃的宽AB为

科目:初中数学 来源: 题型:
 如图,PA、PB分别切⊙O于A、B两点,射线PD与⊙O相交于C,D两点,点E是CD中点,若∠APB=40°,则∠AEP的度数是( )
如图,PA、PB分别切⊙O于A、B两点,射线PD与⊙O相交于C,D两点,点E是CD中点,若∠APB=40°,则∠AEP的度数是( )| A、40° | B、50° |
| C、60° | D、70° |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图:在平面直角坐标系中,A(-2,0),B(0,1),有一组抛物线Ln,它们的顶点Cn(Xn,Yn)在直线AB上,并且经过点(Xn+1,0),当n=1,2,3,4,5…时,Xn=2,3,5,8,13…,根据上述规律,写出抛物线L1的表达式为
如图:在平面直角坐标系中,A(-2,0),B(0,1),有一组抛物线Ln,它们的顶点Cn(Xn,Yn)在直线AB上,并且经过点(Xn+1,0),当n=1,2,3,4,5…时,Xn=2,3,5,8,13…,根据上述规律,写出抛物线L1的表达式为查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,等边△ABC的边长为8,点O为边AC的四等分点(AO<CO),点P为边AB上一动点,连接OP.将△AOP绕点O逆时针旋转,得到△A′OP′,且使得点A′落在边AB上,当点P′落在边BC上时,则AP的长为
如图,等边△ABC的边长为8,点O为边AC的四等分点(AO<CO),点P为边AB上一动点,连接OP.将△AOP绕点O逆时针旋转,得到△A′OP′,且使得点A′落在边AB上,当点P′落在边BC上时,则AP的长为查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com