
【题目】已知AB∥CD,解决下列问题:

(1)如图①,写出∠ABE、∠CDE和∠E之间的数量关系: ;
(2)如图②,BP、DP分别平分∠ABE、∠CDE,若∠E=100°,求∠P的度数;
(3)如图③,若∠ABP=![]() ∠ABE,∠CDP=
∠ABE,∠CDP=![]() ∠CDE,试写出∠P与∠E的数量关系,并说明理由.
∠CDE,试写出∠P与∠E的数量关系,并说明理由.
【答案】(1)∠ABE+∠CDE+∠E=360°;(2)130°;(3)∠P+![]() ∠E=120°,理由见解析
∠E=120°,理由见解析
【解析】
(1)猜想得到三角之间的关系,验证即可;
(2)根据得出三角关系,以及角平分线定义求出四边形PBED中的三个角,进而利用四边形内角和求出所求角的度数即可;
(3)依此类推确定出两角关系,验证即可.
(1)根据题意得:∠ABE+∠CDE+∠E=180°,理由如下:
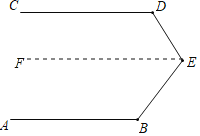
过E作EF∥AB,
∴∠FEB+∠EBA=180°,
∵CD∥AB,EF∥AB,
∴CD∥EF,
∴∠CDE+∠DEF=180°,
∴∠CDE+∠DEB+∠ABE=360°,
故答案为:∠ABE+∠CDE+∠E=360°;
(2)∵BP、DP分别平分∠ABE、∠CDE,
∴∠EDP=![]() ∠CDE,∠EBP=
∠CDE,∠EBP=![]() ∠ABE,即∠CDE=2∠EDP,∠ABE=2∠EBP,
∠ABE,即∠CDE=2∠EDP,∠ABE=2∠EBP,
代入(1)的等式得:2∠EBP+2∠EDP+∠E=360°,
∵∠E=100°,
∴∠EBP+∠EDP=180°﹣![]() ∠E=130°,
∠E=130°,
在四边形PBED中,∠P=360°﹣(∠EBP+∠EDP+∠E)=360°﹣(130°+100°)=130°;
(3)∠P与∠E的数量关系为:∠P+![]() ∠E=120°,理由如下:
∠E=120°,理由如下:
∵∠ABP=![]() ∠ABE,∠CDP=
∠ABE,∠CDP=![]() ∠CDE,
∠CDE,
∴∠CDE=3∠CDP=1.5∠EDP,∠ABE=3∠ABP=1.5∠EBP,
代入(1)的等式得:1.5∠EBP+1.5∠EDP+∠E=360°,
∴∠EBP+∠EDP=240°﹣![]() ∠E,
∠E,
在四边形PBED中,∠P+∠EBP+∠EDP+∠E=360°,
∴∠P+240°﹣![]() ∠E+∠E=360°,即∠P+
∠E+∠E=360°,即∠P+![]() ∠E=120°.
∠E=120°.


科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A. 要了解某公司生产的100万只灯泡的使用寿命,可以采用抽样调查的方法
B. 4位同学的数学期末成绩分别为100、95、105、110,则这四位同学数学期末成绩的中位数为100
C. 甲乙两人各自跳远10次,若他们跳远成绩的平均数相同,甲乙跳远成绩的方差分别为0.51和0.62,则乙的表现较甲更稳定
D. 某次抽奖活动中,中奖的概率为![]() 表示每抽奖50次就有一次中奖
表示每抽奖50次就有一次中奖
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,AC=4,BC=3.点E从点A出发,以每秒4个单位长度的速度沿折线AC-CB运动,到点B停止.当点E不与△ABC的顶点重合时,过点E作其所在直角边的垂线交AB于点F,将△AEF绕点F沿逆时针方向旋转得到△NMF,使点A的对应点N落在射线FE上.设点E的运动时间为t(秒).
(1)用含t的代数式表示线段CE的长.
(2)求点M落到边BC上时t的值.
(3)当点E在边AC上运动时,设△NMF与△ABC重叠部分图形为四边形时,四边形的面积为S(平方单位),求S与t之间的函数关系式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,四边形AOBC是矩形,点O(0,0),点A(5,0),点B(0,3).以点A为中心,顺时针旋转矩形AOBC,得到矩形ADEF,点O,B,C的对应点分别为D,E,F.

(Ⅰ)如图①,当点D落在BC边上时,求点D的坐标;
(Ⅱ)如图②,当点D落在线段BE上时, AD与BC交于点H.
①求证△ADB≌△AOB;
②求点H的坐标.
(Ⅲ)记K为矩形AOBC对角线的交点,S为△KDE的面积,求S的取值范围(直接写出结果即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆客车从甲地开住乙地,一辆出租车从乙地开往甲地,两车同时出发,两车距甲地的距离y(千米)与行驶时间式(小时)之间的函数图象如图所示,则下列说法中错误的是( )
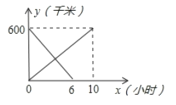
A. 客车比出租车晚4小时到达目的地B. 客车速度为60千米时,出租车速度为100千米/时
C. 两车出发后3.75小时相遇D. 两车相遇时客车距乙地还有225千米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,C为线段AE上一动点(不与点A,E重合),在AE同侧分别作等边△ABC和等边△CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ.则下列结论:①AD=BE;②PQ∥AE;③AP=BQ;④DE=DP.其中正确的是______.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com