
【题目】如图,直线:y=﹣![]() +4与x轴、y轴分别別交于点M、点N,等边△ABC的高为3,边BC在x轴上,将△ABC沿着x轴的正方向平移,在平移过程中,得到△A1B1C1,当点B1与原点O重合时,解答下列问题:
+4与x轴、y轴分别別交于点M、点N,等边△ABC的高为3,边BC在x轴上,将△ABC沿着x轴的正方向平移,在平移过程中,得到△A1B1C1,当点B1与原点O重合时,解答下列问题:
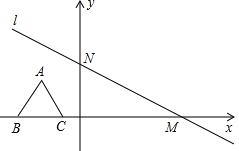
(1)点A1的坐标为 .
(2)求△A1B1C1的边A1C1所在直线的解析式;
(3)若以P、A1、C1、M为顶点的四边形是平行四边形,请直接写出P点坐标.
【答案】(1)(![]() ,3);(2)y=﹣
,3);(2)y=﹣![]() x+6;(3)点P的坐标为:(3
x+6;(3)点P的坐标为:(3![]() ,3)或(5
,3)或(5![]() ,﹣3)或(﹣
,﹣3)或(﹣![]() ,3)
,3)
【解析】
(1)当点B1与原点O重合时,过点A1作A1D⊥x轴于点D,则A1D=3,则B1D=A1Dtan30°=3×![]() =
=![]() ,当x=
,当x=![]() 时,y=﹣
时,y=﹣![]() +4=3=A1D,故点A1在直线上,点A1(
+4=3=A1D,故点A1在直线上,点A1(![]() ,3);
,3);
(2)将点C1(![]() ,0)、A1的坐标代入一次函数表达式y=kx+b,即可求解;
,0)、A1的坐标代入一次函数表达式y=kx+b,即可求解;
(3)分A1C1是平行四边形的边、A1C1是平行四边形的对角线两种情况,分别求解即可.
解:(1)直线:y=﹣![]() +4与x轴、y轴分别別交于点M、点N,
+4与x轴、y轴分别別交于点M、点N,
则点M(4![]() ,0),
,0),
当点B1与原点O重合时,过点A1作A1D⊥x轴于点D,
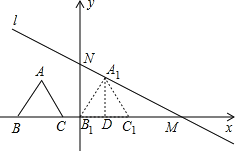
则A1D=3,则B1D=A1Dtan30°=3×![]() =
=![]() ,
,
当x=![]() 时,y=﹣
时,y=﹣![]() +4=3=A1D,故点A1在直线上,
+4=3=A1D,故点A1在直线上,
点A1(![]() ,3),故答案为:(
,3),故答案为:(![]() ,3);
,3);
(2)将点C1(![]() ,0)、A1的坐标代入一次函数表达式:y=kx+b
,0)、A1的坐标代入一次函数表达式:y=kx+b
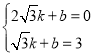
并解得: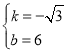
直线A1C1的表达式为:y=﹣![]() x+6;
x+6;
(3)设点P(m,n)
①当A1C1是平行四边形的边时,
则![]() ,0﹣3=n或
,0﹣3=n或![]() ,0+3=n
,0+3=n
解得:m=![]() 或
或![]() ,n=3或﹣3,
,n=3或﹣3,
故点P的坐标为:(![]() ,3)或(
,3)或(![]() ,﹣3);
,﹣3);
②当A1C1是平行四边形的对角线时,
由中点公式得:![]()
解得:m=![]() ,n=3,故点P(
,n=3,故点P(![]() ,3);
,3);
综上点P的坐标为:(3![]() ,3)或(5
,3)或(5![]() ,﹣3)或(﹣
,﹣3)或(﹣![]() ,3).
,3).


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某市去年成功举办2018郴州国际休闲旅游文化节,获评“全国森林旅游示范市”.某市有A,B,C,D,E五个景区很受游客喜爱.一旅行社对某小区居民在暑假期间去以上五个景区旅游(只选一个景区)的意向做了一次随机调查统计,并根据这个统计结果制作了如下两幅不完整的统计图:
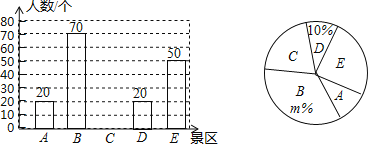
(1)该小区居民在这次随机调查中被调查到的人数是 人,![]() ,并补全条形统计图;
,并补全条形统计图;
(2)若该小区有居民1200人,试估计去B地旅游的居民约有多少人?
(3)小军同学已去过E地旅游,暑假期间计划与父母从A,B,C,D四个景区中,任选两个去旅游,求选到A,C两个景区的概率.(要求画树状图或列表求概率)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O直径,C是⊙O上一点,CO⊥AB于点O,弦CD与AB交于点F,在AB的延长线上取一点E,使EF=ED,过点A作⊙O的切线交ED的延长线于点G.
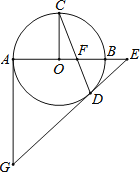
(1)求证:GE是⊙O的切线;
(2)若OF:OB=1:3,⊙O的半径为3,求DE和AG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
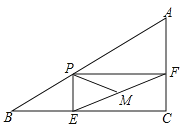
【题目】在Rt△ABC中,∠C=90°,AB=5,AC=3,点P为边AB上一动点(且点P不与点A,B重合),PE⊥BC于E,PF⊥AC于F,点M为EF中点,则PM的最小值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
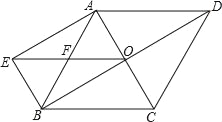
【题目】如图,菱形ABCD对角线交于点O,BE∥AC,AE∥BD,EO与AB交于点F.
(1)求证:EO=DC;
(2)若菱形ABCD的边长为10,∠EBA=60°,求:菱形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
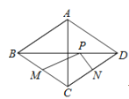
【题目】如图,菱形ABCD中,对角线AC=6,BD=8,M、N分别是BC、CD上的动点,P是线段BD上的一个动点,则PM+PN的最小值是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
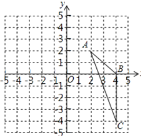
【题目】如图,在平面直角坐标系中,已知![]() 三个顶点的坐标分别是
三个顶点的坐标分别是![]() ,
,![]() ,
,![]() .
.
(1)请在图中画出![]() 向左平移6个单位长度后得到
向左平移6个单位长度后得到![]() ;
;
(2)以点O为位似中心,将![]() 缩小为原来的
缩小为原来的![]() ,得到
,得到![]() ,请在图中y轴右侧,画出
,请在图中y轴右侧,画出![]() ,并求出
,并求出![]() ________.
________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com