
،¾جâؤ؟،؟خھحئ½ّ،°´«ح³خؤ»¯½ّذ£ش°،±»î¶¯£¬خزتذؤ³ضذر§¾ظذذءث،°×ك½ّ¾µن،±ص÷خؤ±ببü£¬بü؛َصûہي²خبüر§ةْµؤ³ة¼¨£¬½«ر§ةْµؤ³ة¼¨·ضخھ![]() ثؤ¸ِµب¼¶£¬²¢½«½ل¹û»وضئ³ة²»حêصûµؤجُذخح³¼ئح¼؛حةبذخح³¼ئح¼£®اë¸ù¾فح³¼ئح¼½â´ًدآءذختجâ:
ثؤ¸ِµب¼¶£¬²¢½«½ل¹û»وضئ³ة²»حêصûµؤجُذخح³¼ئح¼؛حةبذخح³¼ئح¼£®اë¸ù¾فح³¼ئح¼½â´ًدآءذختجâ:

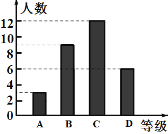
£¨1£©²خ¼سص÷خؤ±ببüµؤر§ةْ¹²سذ بث£»
£¨2£©²¹ب«جُذخح³¼ئح¼£»
£¨3£©شعةبذخح³¼ئح¼ضذ£¬±يت¾![]() µب¼¶µؤةبذخµؤش²ذؤ½اخھ__ ح¼ضذ
µب¼¶µؤةبذخµؤش²ذؤ½اخھ__ ح¼ضذ![]() £»
£»
£¨4£©ر§ذ£¾ِ¶¨´س±¾´خ±ببü»ٌµأ![]() µب¼¶µؤر§ةْضذر،³ِء½أûب¥²خ¼ستذص÷خؤ±ببü£¬زرضھ
µب¼¶µؤر§ةْضذر،³ِء½أûب¥²خ¼ستذص÷خؤ±ببü£¬زرضھ![]() µب¼¶ضذسذؤذةْز»أû£¬إ®ةْء½أû£¬اëسأءذ±ي»ٍ»ت÷×´ح¼µؤ·½·¨اَ³ِثùر،ء½أûر§ةْا،؛أتاز»أûؤذةْ؛حز»أûإ®ةْµؤ¸إآت£®
µب¼¶ضذسذؤذةْز»أû£¬إ®ةْء½أû£¬اëسأءذ±ي»ٍ»ت÷×´ح¼µؤ·½·¨اَ³ِثùر،ء½أûر§ةْا،؛أتاز»أûؤذةْ؛حز»أûإ®ةْµؤ¸إآت£®
،¾´ً°¸،؟£¨1£©30£»£¨2£©ح¼¼û½âخِ£»£¨3£©144،م£¬30£»£¨4£© ![]() £®
£®
،¾½âخِ،؟
£¨1£©¸ù¾فµب¼¶خھAµؤبثت³زشثùص¼µؤ°ظ·ض±ب¼´؟ةاَ³ِ×ـبثت£»
£¨2£©¸ù¾فجُذخح³¼ئح¼µأ³ِA،¢C،¢Dµب¼¶µؤبثت£¬سأ×ـبثت¼ُA،¢C،¢Dµب¼¶µؤبثت¼´؟ة£»
£¨3£©¼ئثمCµب¼¶µؤبثتثùص¼×ـبثتµؤ°ظ·ض±ب£¬¼´؟ةاَ³ِ±يت¾![]() µب¼¶µؤةبذخµؤش²ذؤ½ا؛ح
µب¼¶µؤةبذخµؤش²ذؤ½ا؛ح![]() µؤضµ£»
µؤضµ£»
£¨4£©ہûسأءذ±ي·¨»ٍت÷×´ح¼·¨µأ³ِثùسذµب؟ةؤـµؤاé؟ِت£¬صز³ِز»أûؤذةْ؛حز»أûإ®ةْµؤاé؟ِت£¬¼´؟ةاَ³ِثùاَµؤ¸إآت£®
½â£؛£¨1£©¸ù¾فجâزâµأ³ة¼¨خھAµب¼¶µؤر§ةْسذ3بث£¬ثùص¼µؤ°ظ·ض±بخھ10%£¬
شٍ3،آ10%=30£¬
¼´²خ¼سص÷خؤ±ببüµؤر§ةْ¹²سذ30بث£»
£¨2£©سةجُذخح³¼ئح¼؟ةضھA،¢C،¢Dµب¼¶µؤبثت·ض±ًخھ3بث،¢12بث،¢6بث£¬
شٍ303126=9£¨بث£©£¬¼´Bµب¼¶µؤبثتخھ9بث
²¹ب«جُذخح³¼ئح¼بçدآح¼
£¨3£©![]() £¬
£¬
![]() £¬،àm=30
£¬،àm=30
£¨4£©زہجâز⣬ءذ±يبçدآ:
ؤذ | إ® | إ® | |
ؤذ | (ؤذ£¬إ®) | (ؤذ£¬إ®) | |
إ® | (ؤذ£¬إ®) | (إ®£¬إ®) | |
إ® | (ؤذ£¬إ®) | (إ®£¬إ®) |
سةةد±ي؟ةضھ×ـ¹²سذ6ضض½ل¹û£¬أ؟ضض½ل¹û³ِدضµؤ؟ةؤـذشدàح¬£¬ئنضذثùر،ء½أûر§ةْا،؛أتاز»ؤذز»إ®µؤ½ل¹û¹²سذ4ضض£¬
ثùزش![]() £»
£»
»ٍت÷×´ح¼بçدآ

سةةدح¼؟ةضھ×ـ¹²سذ6ضض½ل¹û£¬أ؟ضض½ل¹û³ِدضµؤ؟ةؤـذشدàح¬£¬ئنضذثùر،ء½أûر§ةْا،؛أتاز»ؤذز»إ®µؤ½ل¹û¹²سذ4ضض£¬
ثùزش![]() £®
£®


 ذ،ر§ةْ10·ضضس؟عثم²âتش100·ضدµءذ´ً°¸
ذ،ر§ةْ10·ضضس؟عثم²âتش100·ضدµءذ´ً°¸
| ؤ꼶 | ¸كضذ؟خ³ج | ؤ꼶 | ³ُضذ؟خ³ج |
| ¸كز» | ¸كز»أâ·ر؟خ³جحئ¼ِ£، | ³ُز» | ³ُز»أâ·ر؟خ³جحئ¼ِ£، |
| ¸ك¶ | ¸ك¶أâ·ر؟خ³جحئ¼ِ£، | ³ُ¶ | ³ُ¶أâ·ر؟خ³جحئ¼ِ£، |
| ¸كب | ¸كبأâ·ر؟خ³جحئ¼ِ£، | ³ُب | ³ُبأâ·ر؟خ³جحئ¼ِ£، |
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛
،¾جâؤ؟،؟2019ؤêµعءù½ىتہ½ç»¥ءھحّ´َ»لشعخعصٍصظ؟ھ£¬ذ،ؤد؛حذ،خ÷²خ¼سءثؤ³·ض»ل³،µؤض¾ش¸·خٌ¹¤×÷£¬±¾´خض¾ش¸·خٌ¹¤×÷ز»¹²ةèضأءثب¸ِ¸عخ»£¬·ض±ًتازµ¼ش±،¢ءھآçش±؛ح×ةر¯ش±£®اëؤمسأ»ت÷×´ح¼»ٍءذ±ي·¨اَ³ِذ،ؤد؛حذ،خ÷ا،؛أ±»·ضإنµ½ح¬ز»¸ِ¸عخ»½ّذذض¾ش¸·خٌµؤ¸إآت£®
²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛
،¾جâؤ؟،؟شعبçح¼µؤص·½ذخحّ¸ٌضذ£¬أ؟ز»¸ِذ،ص·½ذخµؤ±ك³¤¾ùخھ 1£®¸ٌµمب½اذخ ABC£¨¶¥µمتاحّ¸ٌدك½»µمµؤب½اذخ£©µؤ¶¥µم A،¢C µؤ×ّ±ê·ض±ًتا£¨©پ2£¬0£©£¬£¨©پ3£¬3£©£®
£¨1£©اëشعح¼ضذµؤحّ¸ٌئ½أوؤع½¨ء¢ئ½أوض±½ا×ّ±êدµ£¬ذ´³ِµم B µؤ×ّ±ê£»
£¨2£©°ر،÷ABC بئ×ّ±êشµم O ث³ت±صëذ×ھ 90،مµأµ½،÷A1B1C1£¬»³ِ،÷A1B1C1£¬ذ´³ِµم
B1µؤ×ّ±ê£»
£¨3£©زش×ّ±êشµم O خھخ»ثئضذذؤ£¬دàثئ±بخھ 2£¬°ر،÷A1B1C1 ·إ´َخھشہ´µؤ 2 ±¶£¬µأµ½،÷A2B2C2 »³ِ،÷A2B2C2£¬ت¹ثüسë،÷AB1C1 شعخ»ثئضذذؤµؤح¬²à£»
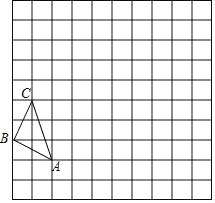
اëشع x ضلةداَ×÷ز»µم P£¬ت¹،÷PBB1 µؤضـ³¤×îذ،£¬²¢ذ´³ِµم P µؤ×ّ±ê£®
²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛
،¾جâؤ؟،؟إذ¶د¹طسعxµؤ·½³جmx2+£¨2m©پ1£©x+m+3£½0µؤ¸ùµؤاé؟ِ£¬²¢ض±½سذ´³ِ¹طسعxµؤ·½³جmx2+£¨2m©پ1£©x+m+3£½0µؤ¸ù¼°دàس¦µؤmµؤب،ضµ·¶خ§£®
²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛
،¾جâؤ؟،؟ؤ³سخہضش°سذز»¸ِض±¾¶خھ16أ×µؤش²ذخإçث®³ط£¬إçث®³طµؤضـ±كسذز»ب¦إçث®ح·£¬إç³ِµؤث®ضùخھإ×خïدك£¬شع¾àث®³طضذذؤ3أ×´¦´ïµ½×î¸ك£¬¸ك¶بخھ5أ×£¬از¸÷·½دٍإç³ِµؤث®ضùا،؛أشعإçث®³طضذذؤµؤ×°تخخï´¦»ط؛د£¬بçح¼ثùت¾£¬زشث®ئ½·½دٍخھ![]() ضل£¬إçث®³طضذذؤخھشµم½¨ء¢ئ½أوض±½ا×ّ±êدµ.
ضل£¬إçث®³طضذذؤخھشµم½¨ء¢ئ½أوض±½ا×ّ±êدµ.
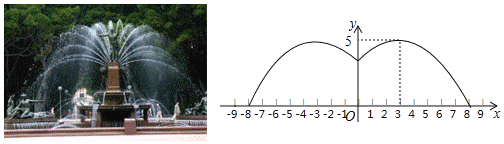
£¨1£©اَث®ضùثùشعإ×خïدك£¨µعز»دَدق²؟·ض£©µؤ؛¯ت±ي´ïت½£»
£¨2£©حُت¦¸µشعإçث®³طؤعخ¬ذقة豸ئع¼ن£¬إçث®¹ـزâحâإçث®£¬خھءث²»±»ءـتھ£¬ةي¸ك1.8أ×µؤحُت¦¸µص¾ء¢ت±±طذëشعہëث®³طضذذؤ¶àةظأ×زشؤع£؟
²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛
،¾جâؤ؟،؟بçح¼£¬![]() £¬
£¬![]() ئ½·ض
ئ½·ض![]() £¬از½»
£¬از½»![]() سعµم
سعµم![]() £¬
£¬![]() ئ½·ض
ئ½·ض![]() £¬از½»
£¬از½»![]() سعµم
سعµم![]() £¬
£¬![]() سë
سë![]() دཻسعµم
دཻسعµم![]() £¬ء¬½س
£¬ء¬½س![]()

![]() اَ
اَ![]() µؤ¶بت£»
µؤ¶بت£»
![]() اَض¤£؛ثؤ±كذخ
اَض¤£؛ثؤ±كذخ![]() تاءâذخ£®
تاءâذخ£®
²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛
،¾جâؤ؟،؟بçح¼ثùت¾خھء½°ر°´²»ح¬±بہ³ك½ّذذ؟ج¶بµؤض±³ك£¬أ؟°رض±³كµؤ؟ج¶ب¶¼تا¾ùشبµؤ£¬زرضھء½°رض±³كشع؟ج¶ب10´¦تا¶شئëµؤ£¬ازةدأوµؤض±³كشع؟ج¶ب15´¦سëدآأوµؤض±³كشع؟ج¶ب18´¦ز²¸ص؛أ¶شئ룬شٍةدأوض±³كµؤ؟ج¶ب16سëدآأوض±³ك¶شس¦µؤ؟ج¶بتا£¨ £©
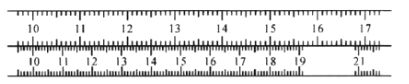
A.19.4B.19.5C.19.6D.19.7
²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛
،¾جâؤ؟،؟بçح¼£¬زرضھصب½اذخABCµؤ±ك³¤ABتا480؛ءأ×£®ز»ضتµمD´سµمB³ِ·¢£¬رطBA·½دٍ£¬زشأ؟أëضس10؛ءأ×µؤثظ¶بدٍµمAشث¶¯£®
£¨1£©½¨ء¢؛دتتµؤض±½ا×ّ±êدµ£¬سأشث¶¯ت±¼نt£¨أ룩±يت¾µمDµؤ×ّ±ê£»
£¨2£©¹µمDشعب½اذخABCµؤؤع²؟×÷ز»¸ِ¾طذخDEFG£¬ئنضذEFشعBC±كةد£¬GشعAC±كةد£®شعح¼ضذصز³ِµمD£¬ت¹¾طذخDEFGتاص·½ذخ£¨زھاَثù±ي´ïµؤ·½ت½ؤـجهدض³ِصزµمDµؤ¹³ج£©£»
£¨3£©¹µمD،¢B،¢C×÷ئ½ذذثؤ±كذخ£¬µ±tخھ؛خضµت±£¬سةµمC،¢B،¢D،¢F×é³ةµؤئ½ذذثؤ±كذخµؤأو»µبسعب½اذخADCµؤأو»£¬²¢اَ´ثت±µمFµؤ×ّ±ê£®

²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛
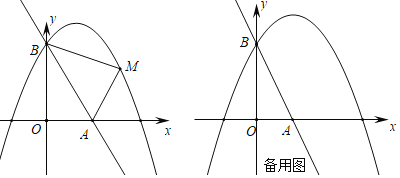
،¾جâؤ؟،؟بçح¼£¬ض±دكl£؛y£½©پ3x+3سëxضل،¢yضل·ض±ًدཻسعA،¢Bء½µم£¬إ×خïدكy£½ax2©پ2ax©پ3a£¨a£¼0£©¾¹µمB£®
£¨1£©اَ¸أإ×خïدكµؤ؛¯ت±ي´ïت½£»
£¨2£©زرضھµمMتاإ×خïدكةدµؤز»¸ِ¶¯µم£¬²¢ازµمMشعµعز»دَدقؤع£¬ء¬½سAM،¢BM£¬ةèµمMµؤ؛ل×ّ±êخھm£¬،÷ABMµؤأو»خھS£¬اَSسëmµؤ؛¯ت±ي´ïت½£¬²¢اَ³ِSµؤ×î´َضµ£»
£¨3£©شع£¨2£©µؤجُ¼دآ£¬µ±Sب،µأ×î´َضµت±£¬¶¯µمMدàس¦µؤخ»ضأ¼اخھµمM،ن£®½«ض±دكlبئµمA°´ث³ت±صë·½دٍذ×ھµأµ½ض±دكl،ن£¬µ±ض±دكl،نسëض±دكAM،نضط؛دت±ح£ض¹ذ×ھ£¬شعذ×ھ¹³جضذ£¬ض±دكl،نسëدك¶خBM،ن½»سعµمC£¬ةèµمB،¢M،نµ½ض±دكl،نµؤ¾àہë·ض±ًخھd1،¢d2£¬µ±d1+d2×î´َت±£¬اَض±دكl،نذ×ھµؤ½ا¶ب£¨¼´،دBACµؤ¶بت£©£®
²é؟´´ً°¸؛ح½âخِ>>
¹ْ¼تر§ذ£سإر، - ء·د°²لءذ±ي - تشجâءذ±ي
؛±±ت،»¥ءھحّخ¥·¨؛ح²»ء¼ذإد¢¾ظ±¨ئ½ج¨ | حّةدسذ؛¦ذإد¢¾ظ±¨×¨اّ | µçذإص©ئ¾ظ±¨×¨اّ | ةوہْت·ذéخقض÷زهسذ؛¦ذإد¢¾ظ±¨×¨اّ | ةوئَاضب¨¾ظ±¨×¨اّ
خ¥·¨؛ح²»ء¼ذإد¢¾ظ±¨µç»°£؛027-86699610 ¾ظ±¨ستدن£؛58377363@163.com