已知.如下图.我们可以用长度相同的火柴棒按一定规律拼搭正多边形组成图案.图案①需8根火柴棒.图案②需15根火柴棒.-.按此规律.搭建第n个图案需要7n+1根火柴棒.搭建第2017个图案需要14120根火柴棒．题目和参考答案——青夏教育精英家教网—

12．已知，如下图，我们可以用长度相同的火柴棒按一定规律拼搭正多边形组成图案，图案①需8根火柴棒，图案②需15根火柴棒，…，按此规律，搭建第n个图案需要7n+1根火柴棒，搭建第2017个图案需要14120根火柴棒．

分析（1）根据图案①、②、③中火柴棒的数量可知，第1个图形中火柴棒有8根，每多一个多边形就多7根火柴棒，由此可知第n个图案需火柴棒8+7（n-1）=7n+1根；
（2）根据（1）的结果，当n=2017时可得结果．

解答解：（1）∵图案①需火柴棒：8根；
图案②需火柴棒：8+7=15根；
图案③需火柴棒：8+7+7=22根；
…
∴图案n需火柴棒：8+7（n-1）=7n+1根；

（2）当n=2017时，7n+1=7×2017+1=14120，
∴搭建第2017个图案需要14120根火柴棒；
故答案为：7n+1；14120．

点评本题主要考查了图形的变化规律，发现第n个图案需要7n+1根火柴是解答此题的关键．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：解答题

2．

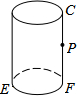如图：有一个圆柱，底面圆的直径EF=$\frac{16}{π}$，高FC=12cm，P为FC的中点，求蚂蚁从E点爬到P点的最短距离是多少？（画出平面图形）

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

3．如图1和图2，AB是⊙O的直径，AB=10，C是⊙O上的一点，将$\widehat{BC}$沿弦BC翻折，交AB于点D．
（1）若点D与圆心O重合，直接写出∠B的度数；
（2）设CD交⊙O于点E，若CE平分∠ACB，
①求证：△BDE是等腰三角形；
②求△BDE的面积；
（3）将图1中的$\widehat{BD}$沿直径AB翻折，得到图2，若点F恰好是翻折后的$\widehat{BD}$的中点，直接写出∠B的度数．

查看答案和解析>>

科目：初中数学 来源： 题型：选择题

20．计算|-6|-（-$\frac{1}{3}$）⁰的值是（　　）

A．

B．

-5

C．

5$\frac{2}{3}$

D．

查看答案和解析>>

科目：初中数学 来源： 题型：选择题

7．若关于x的一元二次方程$\frac{\sqrt{3}}{4}$x²+$\sqrt{3}$x+tana=0有两个相等的实数根，则锐角a等于（　　）

A．

15°

B．

30°

C．

45°

D．

60°

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

17．

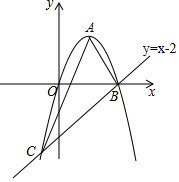如图，已知抛物线y=-x²+2x经过原点O，且与直线y=x-2交于B，C两点．
（1）求抛物线的顶点A的坐标及点B，C的坐标；
（2）求证：∠ABC=90°；
（3）在直线BC上方的抛物线上是否存在点P，使△PBC的面积最大？若存在，请求出点P的坐标；若不存在，请说明理由；
（4）若点N为x轴上的一个动点，过点N作MN⊥x轴与抛物线交于点M，则是否存在以O，M，N为顶点的三角形与△ABC相似？若存在，请求出点N的坐标；若不存在，请说明理由．

查看答案和解析>>

科目：初中数学 来源： 题型：填空题

4．如果关于x的一元二次方程kx²-3x-1=0无实数根，那么k的取值范围是k＜-$\frac{9}{4}$．

查看答案和解析>>

科目：初中数学 来源： 题型：选择题

1．