
分析 先算括号里面的,再算除法,最后求出x、y的值代入进行计算即可.
解答 解:原式=$\frac{x+y}{x-y}$-$\frac{x-2y}{x-y}$
=$\frac{x+y-x+2y}{x-y}$
=$\frac{3y}{x-y}$,
∵$\sqrt{2-x}$与$\sqrt{2x-4}$有意义,
∴$\left\{\begin{array}{l}{2-x≥0}\\{2x-4≥0}\end{array}\right.$,解得x=2,
∴y=3,
∴原式=$\frac{9}{2-3}$=-9.
点评 本题考查的是分式的化简求值,分式求值题中比较多的题型主要有三种:转化已知条件后整体代入求值;转化所求问题后将条件整体代入求值;既要转化条件,也要转化问题,然后再代入求值.


科目:初中数学 来源: 题型:解答题
 某校举办了主题为“将根值于母校,把爱常留心中”的捐种毕业树活动,学生会对毕业班学生自愿捐款活动进行了抽样调查,得到一组学生捐款情况的数据,如图是根据这组数据绘制的统计图,图中从左到右各长方形高度之比为3:4:5:7:2,又知此次调查中捐50元和100元的人数共36人.
某校举办了主题为“将根值于母校,把爱常留心中”的捐种毕业树活动,学生会对毕业班学生自愿捐款活动进行了抽样调查,得到一组学生捐款情况的数据,如图是根据这组数据绘制的统计图,图中从左到右各长方形高度之比为3:4:5:7:2,又知此次调查中捐50元和100元的人数共36人.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
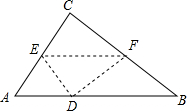 如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,翻折∠C,使点C落在斜边AB上某一点D处,折痕为EF(点E、F分别在边AC、BC上).若△CEF与△ABC相似,则AD的长为$\frac{18}{5}$或5.
如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,翻折∠C,使点C落在斜边AB上某一点D处,折痕为EF(点E、F分别在边AC、BC上).若△CEF与△ABC相似,则AD的长为$\frac{18}{5}$或5.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
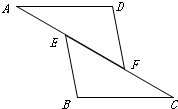 如图所示,在△AFD和△BEC中,点A、E、F、C在同一条直线上,有下面四个论断:(1)AD=CB,(2)AE=CF,(3)∠B=∠D,(4)AD∥BC,
如图所示,在△AFD和△BEC中,点A、E、F、C在同一条直线上,有下面四个论断:(1)AD=CB,(2)AE=CF,(3)∠B=∠D,(4)AD∥BC,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com