
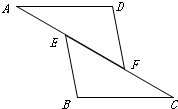
 如图所示,在△AFD和△BEC中,点A、E、F、C在同一条直线上,有下面四个论断:(1)AD=CB,(2)AE=CF,(3)∠B=∠D,(4)AD∥BC,
如图所示,在△AFD和△BEC中,点A、E、F、C在同一条直线上,有下面四个论断:(1)AD=CB,(2)AE=CF,(3)∠B=∠D,(4)AD∥BC,分析 选择①②④得到③,组成命题为如果AD=CB,AE=CF,AD∥BC,那么∠D=∠B;利用“SAS”证明△ADF≌△CBE,然后根据相似的性质得到∠D=∠B.
解答 解:题设:(1)(2)(4);
结论:(3).
证明如下:∵AD∥BC,
∴∠A=∠C,
∵AE=CF,
∴AE+EF=EF+CF,
∴AF=CE,
在△ADF和△CBE中,
$\left\{\begin{array}{l}{AD=CB}\\{∠A=∠C}\\{AF=CE}\end{array}\right.$,
∴△ADF≌△CBE(SAS),
∴∠D=∠B.
故答案为:(1)(2)(4);(3).
点评 本题考查了全等三角形的判定与性质:判断三角形全等的方法有“SSS”、“SAS”、“ASA”、“AAS”;全等三角形的对应角相等,对应边相等.


 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com