
����Ŀ��2018�����������п��ܷ�60�֣���������1000����Ϊ��ѡ��Ŀ������������Զ��������ʵ������Զ���������������������ѡ�����Ů��800����Ϊ��ѡ��Ŀ������������Զ�������������������������������������ѡ������![]() ijУ�Ե÷ֳ���40�ֵ�20λѧ���ijɼ�m����ͳ�ƣ������Ƶ���ֲ�����ʾ��
ijУ�Ե÷ֳ���40�ֵ�20λѧ���ijɼ�m����ͳ�ƣ������Ƶ���ֲ�����ʾ��

![]() ��a��ֵ��
��a��ֵ��
![]() ��������ͼ���������������
��������ͼ���������������![]() ������Ӧ������ͼ��Բ�ĽǵĴ�С��
������Ӧ������ͼ��Բ�ĽǵĴ�С��
![]() ������С���ڸտ�ʼѵ��ʱ��ѡ����Ŀ���ѡ���������ѵ���������оٷ���С��ѡ��������
������С���ڸտ�ʼѵ��ʱ��ѡ����Ŀ���ѡ���������ѵ���������оٷ���С��ѡ��������![]() �����������ĸ���
�����������ĸ���![]() ��ʾ����������ĸ��ʾ������Ŀ
��ʾ����������ĸ��ʾ������Ŀ![]()

���𰸡���1��a=9����2��![]() ����3������С��ѡ��������
����3������С��ѡ��������![]() �����������ĸ���Ϊ
�����������ĸ���Ϊ![]() ��
��
��������
![]() ���ݸ�������֮�͵������������ɵ�a��ֵ��
���ݸ�������֮�͵������������ɵ�a��ֵ��
![]() ��
��![]() ���Եڶ�������ռ�������ı����ɵã�
���Եڶ�������ռ�������ı����ɵã�
![]() ���ȸ������⻭����״ͼ��Ȼ������״ͼ������еȿ��ܵĽ����С��ѡ��������
���ȸ������⻭����״ͼ��Ȼ������״ͼ������еȿ��ܵĽ����С��ѡ��������![]() ������������������������ø��ʹ�ʽ������ô𰸣�
������������������������ø��ʹ�ʽ������ô𰸣�
![]() ��
��
![]() ������
������![]() ������Ӧ������ͼ��Բ�ĽǵĴ�СΪ
������Ӧ������ͼ��Բ�ĽǵĴ�СΪ![]() ��
��
![]() ��������Զ��������ʵ������Զ�������������������ֱ��ΪA��B��C��D��E��
��������Զ��������ʵ������Զ�������������������ֱ��ΪA��B��C��D��E��
������״ͼ��ͼ��ʾ��

����20��ѡ������С��ѡ��������![]() ��������������2�ֽ����
��������������2�ֽ����
����С��ѡ��������![]() �����������ĸ���Ϊ
�����������ĸ���Ϊ![]() ��
��


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У���ACB=90����AC=BC��BE��CE��E��AD��CE��D��

��1����֤����ADC�ա�CEB��
��2��AD=5cm��DE=3cm����BE�ij��ȣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ����в��ϣ�
С������һ�����⣺��֪����ͼ1������ABC�У���BAC=120��,��ABC=40�����Թ���ABC��һ�����㻭һ��ֱ�ߣ����������ηָ����������������.
���������ǣ���ͼ2�����ȱ�����С�ǡ�C��Ȼ��������ζ���A��ֱ�߽�BC�ڵ�D. ����BAC�ֳ������ǣ�ʹ��DAC=20������ABC���ɱ��ָ����������������.
ϲ�����Խ��С���ּ���̽�������������ڽ��е�����������������������ϵʱ����������һ�����Ա��������һ��ֱ�߷ָ����������������.
���������ǣ�

��ͼ3���Ȼ���ADC ��ʹDA=DC���ӳ�AD����B��ʹ��BCDҲ�ǵ��������Σ����DC=BC����ô��CDB =��ABC����Ϊ��CDB=2��A�����ԡ�ABC= 2��A������С���õ���һ�����ۣ�
������������һ��������С�ǵ�2��ʱ�����������һ�����Ա��������һ��ֱ�߷ָ���������������Σ�
����ο�С������������̽�������������ڽ��е�����������������������ϵʱ����������һ�����Ա��������һ��ֱ�߷ָ����������������.��ֱ��д������̽�����������������ۣ�����д��̽�����̻����ɣ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�ضԽ���AC�������ٰѡ�ACD��CA����ƽ�Ƶõ���A1C1D1������AD1��BC1����֪��ACB=30�㣬AB=1��
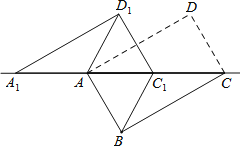
��1����֤����A1AD1�ա�CC1B��
��2����CC1=1ʱ����֤���ı���ABC1D1��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD�����Ϊ1cm2���Խ��߽��ڵ�O����AB��AOΪ�ڱ���ƽ���ı���AOC1B���Խ��߽��ڵ�O1����AB��AO1Ϊ�ڱ���ƽ���ı���AO1C2B�����������ƣ���ƽ���ı���AO2016C2017B�����Ϊ_____��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����x��һԪ���η���x2+2x+m��2=0������ʵ������mΪ���������Ҹ÷��̵ĸ��������������������������������m�ĺ�Ϊ��������
A. 6 B. 5 C. 4 D. 3
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���߳�Ϊ2��������OABC��ƽ��ֱ������ϵ��λ��x���Ϸ���OA��x���������ļн�Ϊ60������B�������Ϊ_____.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ʵ������������ x(x 0), y( y 0) ��һ���Ӧֵ���±���
x | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
y | 7 | 3.5 | 2.33 | 1.75 | 1.4 | 1.17 | 1 |
��1���������н���ƽ��ֱ������ϵ��������Ӧ�ĺ���ͼ����������������ʽ��
��2����Ϻ���ͼ�������⣺���������һλС����

��![]() ��ֵԼΪ���٣�
��ֵԼΪ���٣�
�ڵ�A����Ϊ��6,0������B�ں���ͼ���ϣ�OA=OB,���B�ĺ�����Լ�Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
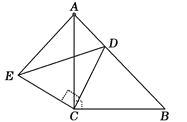
����Ŀ����ͼ����ACB����ECD���ǵ���ֱ�������Σ���ACB=��ECD=90����DΪAB����һ�㣮
��֤����1����ACE�ա�BCD����2��![]() ��
��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com