Question

15．边长分别为3、4、5的三角形的内心到一边的距离是1．

Answer 1

分析 首先证明△ABC是直角三角形，再利用$\frac{1}{2}$•AB•r+$\frac{1}{2}$•BC•r+$\frac{1}{2}$•AC•r=$\frac{1}{2}$•BC•AC即可解决．

解答 解：如图，⊙O是△ABC的内切圆，切点分别为E、F、G．
∵AB=5，AC=3，BC=4，
∴AC²+BC²=AB²，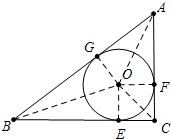
∴∠ACB=90°，
设OG=OE=OF=r，
∵$\frac{1}{2}$•AB•r+$\frac{1}{2}$•BC•r+$\frac{1}{2}$•AC•r=$\frac{1}{2}$•BC•AC，
∴5r+4r+3r=12，
∴r=1．
故答案为1．

点评 本题考查三角形内心、勾股定理的逆定理，解题关键是判断三角形是直角三角形，学会用面积法求内切圆半径，属于中考常考题型．