
【题目】在△ABC中,D是BC上一点,且BD=2DC,E是AD的中点,旋转过E点的直线l.

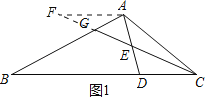
(1)如图1,当l经过C,交AB于G,求证:BG=3AG;
(2)如图2,当l平分△ABC的面积,分别交BC,AC于M,N,求![]() 的值;
的值;
(3)若AB=8,AC=6,BC=12,且l平分△ABC的周长,分别交BC,AD于M,N,直接写出BM的长.
【答案】(1)见解析;(2)![]() =
=![]() ;(3)BM=
;(3)BM=![]() .
.
【解析】
(1)过点A作BC的平行线AF,利用点E是AD中点构造△AEF≌△DEC,得到AF=CD,即BC=3AF.又由平行得△AFG∽△BCG,即得到BG与AG的比即为相似比等于BC与AF的比,得证.
(2)连接CE与BE,由AE=DE可得等底同高的△AEC与△DEC面积相等;由BD=2DC可得同高的△ABD与△ACD面积有2倍关系.故可设这最小的两个△AEN与△CEN的面积分别为a和b,用a和b表示图中所有三角形面积.过点A作BC平行线AG,构造△AEH≌△DEM与△ANH∽△CNM,根据面积比求得△ANH与△CNM的相似比,进而求得a与b的关系.而![]() 可看作同高的△BME与△CME的面积比,根据a与b的关系即能求得.
可看作同高的△BME与△CME的面积比,根据a与b的关系即能求得.
(3)构造△AEH≌△DEM与△ANH∽△CNM,设AH=DM=x,用x表示△ABC三边上的线段,再利用△ANH∽△CNM的对应边成比例列得关于x的方程,求出x即求得BM的长.
解:(1)证明:过点A作AF∥BC,交CG延长线与点F
∴∠F=∠DCE
∵点E是AD中点
∴AE=DE
在△AEF与△DEC中
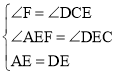 ,
,
∴△AEF≌△DEC(AAS)
∴AF=CD
∵BD=2DC
∴BC=BD+DC=3DC=3AF
∵AF∥BC
∴△AFG∽△BCG
∴![]()
∴BG=3AG
(2)过点A作AH∥BC,交直线MN与点H,连接BE、CE
∴∠H=∠DME
∵点E是AD中点
∴AE=DE
在△AEH与△DEM中
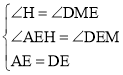
∴△AEH≌△DEM(AAS)
∴S△AEH=S△DEM
设S△AEN=a,S△CEN=b
∴S△AEC=S△AEN+S△CEN=a+b
∴S△DEC=S△AEC=a+b,S△DEB=S△AEB
∴S△ACD=S△DEC+S△AEC=2a+2b
∵BD=2DC
∴S△ABD=2S△ACD=4a+4b
∴S△DEB=S△AEB=![]() S△ABD=2a+2b,S△ABC=S△ABD+S△ACD=6a+6b
S△ABD=2a+2b,S△ABC=S△ABD+S△ACD=6a+6b
∵直线MN平分S△ABC
∴S四边形ABMN=S△CMN=![]() S△ABC=3a+3b
S△ABC=3a+3b
∴S△BEM=S四边形ABMN﹣S△ABE﹣S△AEN=3a+3b﹣(2a+2b)﹣a=b,S△DEM=S△CMN﹣S△DEC﹣S△CEN=3a+3b﹣(a+b)﹣b=2a+b
∴S△AEH=S△DEM=2a+b
∴S△ANH=S△AEH﹣S△AEN=2a+b﹣a=a+b
∵AH∥BC
∴△ANH∽△CNM
∴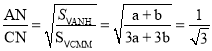
∴![]()
即![]() a
a
∴![]()
![]()
![]() ,
,
∴![]() 的值为
的值为![]() ;
;

(3)过点A作AH∥BC,交直线MN与点H,
由(2)得:△AEH≌△DEM,△ANH∽△CNM
∴设AH=DM=x
∵BC=12,BD=2DC
∴DC=4,BD=8
∴BM=BD﹣MD=8﹣x,CM=DC+MD=4+x
∵直线MN平分△ABC周长,AB=8,AC=6
∴MD+DC+CN=AN+AB+BM=![]() (AB+AC+BC)=13
(AB+AC+BC)=13
∴CN=13﹣MD﹣CD=13﹣x﹣4=9﹣x,AN=13﹣AB﹣BM=13﹣8﹣(8﹣x)=x﹣3
∵△ANH∽△CNM
∴![]()
∴![]()
解得:x1=![]() ,x2=
,x2=![]() (舍去)
(舍去)
∴BM![]()



 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案科目:初中数学 来源: 题型:
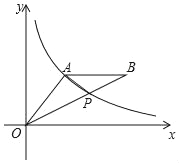
【题目】如图,A(3,m)是反比例函数y=![]() 在第一象限图象上一点,连接OA,过A作AB∥x轴,连接OB,交反比例函数y=
在第一象限图象上一点,连接OA,过A作AB∥x轴,连接OB,交反比例函数y=![]() 的图象于点P(2
的图象于点P(2![]() ,
,![]() ).
).
(1)求m的值和点B的坐标;
(2)连接AP,求△OAP的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
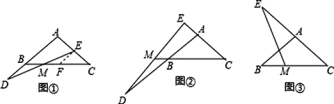
【题目】已知,在△ABC中,AB=AC,在射线AB上截取线段BD,在射线CA上截取线段CE,连结DE,DE所在直线交直线BC于点M.
猜想:当点D在边AB的延长线上,点E在边AC上时,过点E作EF∥AB交BC于点F,如图①.若BD=CE,则线段DM、EM的大小关系为 .
探究:当点D在边AB的延长线上,点E在边CA的延长线上时,如图②.若BD=CE,判断线段DM、EM的大小关系,并加以证明.
拓展:当点D在边AB上(点D不与A、B重合),点E在边CA的延长线上时,如图③.若BD=1,CE=4,DM=0.7,求EM的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
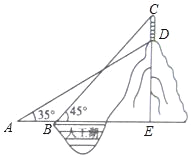
【题目】某公园的人工湖边上有一座假山,假山顶上有一竖起的建筑物CD,高为10米,数学小组为了测量假山的高度DE,在公园找了一水平地面,在A处测得建筑物点D(即山顶)的仰角为35°,沿水平方向前进20米到达B点,测得建筑物顶部C点的仰角为45°,求假山的高度DE.(结果精确到1米,参考数据:sin35°≈![]() ,cos35°≈
,cos35°≈![]() ,tan35°≈
,tan35°≈![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有七张正面分别标有数字﹣3,﹣2,﹣1,0,1,2,3的卡片,它们除数字不同外其余全部相同.现将它们背面朝上,洗匀后从中随机抽取一张,记卡片上的数字为a,则使关于x的一元二次方程x2﹣2(a﹣1)x+a(a﹣3)=0有两个不相等的实数根,且以x为自变量的二次函数y=x2﹣(a2+1)x﹣a+2的图象不经过点(1,0)的概率是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P从![]() 出发,沿所示方向运动,每当碰到长方形OABC的边时会进行反弹,反弹时反射角等于入射角,当点P第2018次碰到长方形的边时,点P的坐标为______.
出发,沿所示方向运动,每当碰到长方形OABC的边时会进行反弹,反弹时反射角等于入射角,当点P第2018次碰到长方形的边时,点P的坐标为______.

【答案】![]()
【解析】
根据反射角与入射角的定义作出图形;由图可知,每6次反弹为一个循环组依次循环,用2018除以6,根据商和余数的情况确定所对应的点的坐标即可.
解:如图所示:经过6次反弹后动点回到出发点![]() ,
,
![]() ,
,
![]() 当点P第2018次碰到矩形的边时为第337个循环组的第2次反弹,
当点P第2018次碰到矩形的边时为第337个循环组的第2次反弹,
![]() 点P的坐标为
点P的坐标为![]() .
.
故答案为:![]() .
.
【点睛】
此题主要考查了点的坐标的规律,作出图形,观察出每6次反弹为一个循环组依次循环是解题的关键.
【题型】填空题
【结束】
15
【题目】为了保护环境,某公交公司决定购买A、B两种型号的全新混合动力公交车共10辆,其中A种型号每辆价格为a万元,每年节省油量为![]() 万升;B种型号每辆价格为b万元,每年节省油量为
万升;B种型号每辆价格为b万元,每年节省油量为![]() 万升:经调查,购买一辆A型车比购买一辆B型车多20万元,购买2辆A型车比购买3辆B型车少60万元.
万升:经调查,购买一辆A型车比购买一辆B型车多20万元,购买2辆A型车比购买3辆B型车少60万元.
![]() 请求出a和b;
请求出a和b;
![]() 若购买这批混合动力公交车每年能节省
若购买这批混合动力公交车每年能节省![]() 万升汽油,求购买这批混合动力公交车需要多少万元?
万升汽油,求购买这批混合动力公交车需要多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
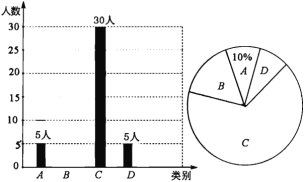
【题目】央视“经典咏流传”开播以来受到社会广泛关注.我市某校就“中华文化我传承——地方戏曲进校园”的喜爱情况进行了随机调查,对收集的信息进行统计,绘制了下面两副尚不完整的统计图.请你根据统计图所提供的信息解答下列问题:
图中A表示“很喜欢”,B表示“喜欢”,C表示“一般”,D表示“不喜欢”.
(1)被调查的总人数是_____________人,扇形统计图中C部分所对应的扇形圆心角的度数为_______.
(2)补全条形统计图;
(3)若该校共有学生1800人,请根据上述调查结果,估计该校学生中A类有__________人;
(4)在抽取的A类5人中,刚好有3个女生2个男生,从中随机抽取两个同学担任两角色,用树形图或列表法求出被抽到的两个学生性别相同的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com