
 ��ͼ����ƽ��ֱ������ϵ�У���O������ԭ�㣬�ı���ABCD�����Σ���B����C��x���ϣ���A��y���ϣ�BD��y���ڵ�M����A������Ϊ��0��4������B������Ϊ��-3��0����
��ͼ����ƽ��ֱ������ϵ�У���O������ԭ�㣬�ı���ABCD�����Σ���B����C��x���ϣ���A��y���ϣ�BD��y���ڵ�M����A������Ϊ��0��4������B������Ϊ��-3��0����| 5 |
| 3 |
| 2 |
| 3 |
| 2 |
| 5 |
| 2 |
| AP |
| AO |
| AM |
| AP |
| AO2+BO2 |
| 42+(-3)2 |
|
|
| 1 |
| 2 |
| 3 |
| 2 |
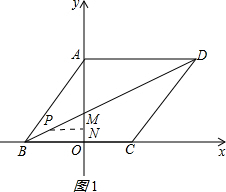 ��
��| 3 |
| 2 |
| 3 |
| 2 |
| 5 |
| BO2+OM2 |
3
| ||
| 2 |
3
| ||||
| 2 |
| PM |
| BM |
| MN |
| MO |
| ||||||
|
| y | ||
|
| 3 |
| 2 |
| 3 |
| 2 |
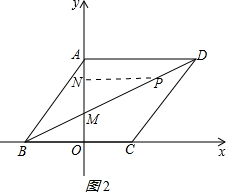 ��
��| 5 |
3
| ||
| 2 |
| 3 |
| 2 |
| 5 |
| 2 |
| AM2+AD2 |
5
| ||
| 2 |
| PM |
| MD |
| MN |
| AM |
| ||||||
|
| y | ||
|
| 3 |
| 2 |
| 3 |
| 2 |
| 5 |
| 2 |
|
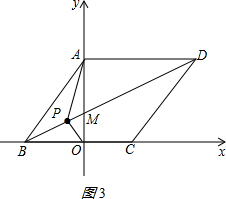 ��
��| 5 |
| 2 |
| AP |
| AM |
| AO |
| AP |
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 5 |
| 2 |
| (-1+3)2+12 |
| 5 |
| ||
|


 �̲�ȫ���ִʾ�ƪϵ�д�
�̲�ȫ���ִʾ�ƪϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
| A��-y | B��y | C��-xy | D��xy |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
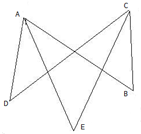 �߶�AB��CD�ཻ�ڵ�O��AEƽ�֡�BCD��CEƽ�֡�BCD������B=�����ǡ�D=��ʱ����E�Ķ���Ϊ
�߶�AB��CD�ཻ�ڵ�O��AEƽ�֡�BCD��CEƽ�֡�BCD������B=�����ǡ�D=��ʱ����E�Ķ���Ϊ�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
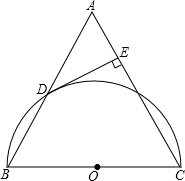 ��֪��ABC�У�AB=AC��DE��AC�ڵ�E��DE����O�����ڵ�D��
��֪��ABC�У�AB=AC��DE��AC�ڵ�E��DE����O�����ڵ�D���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
 ij��·��һ����������״������ABC����������ͼ��ʾ����ͼ�н�����ֱ������ϵ�У������ߵĽ���ʽΪy=-
ij��·��һ����������״������ABC����������ͼ��ʾ����ͼ�н�����ֱ������ϵ�У������ߵĽ���ʽΪy=-| 1 |
| 10 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
| 1 |
| 2 |
| 3 |
| 2 |

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com