
����Ŀ��Ϊ�˼�ǿ����Ľ�ˮ��ʶ����������ˮ��Դ��ij�в��ü۸���ص��ֶδﵽ��ˮ��Ŀ�ģ���������ˮ�շѵ��շѱ����±���

���磺ij������1�·���ˮ8�����ף�Ӧ��ˮ��Ϊ2��6+4����8-6��=20��Ԫ����
������ϱ������ݽ���������⣺
��1����ij������2�·���ˮ5�����ף���Ӧ��ˮ�Ѷ���Ԫ��
��2����ij������3�·ݽ�ˮ��36Ԫ������ˮ��Ϊ���������ף�
��3����ij������4�·���ˮa������������6��a��10�������ú�a�Ĵ���ʽ��ʾӦ��ˮ����
��4����ij������5��6�����¹���ˮ18��������6�·���ˮ��������10������������5�·���ˮx�����ף����ú�x�Ĵ���ʽ��ʾ�û�����5��6�����¹���ˮ�Ѷ���Ԫ��
���𰸡���1�� 10Ԫ����2�� 11�����ף���3����4a-12��Ԫ����4�� ��5�·ݲ�����6m3ʱ��ˮ��Ϊ��-6x+92��Ԫ����5�·ݳ���6m3ʱ��ˮ��Ϊ��-4x+80��Ԫ��
��������
�����������1����2��������ˮ���ķ�Χȷ���������������ɣ�
��3��36Ԫһ����ˮ������10�����ף��ֶμ��㼴�ɣ�
��4����5�·ݲ�����6m3ʱ��5�·ݳ���6m3ʱ���������ʽ������
�����������1��2��5=10Ԫ
��Ӧ��ˮ��10Ԫ��
��2��10+��36-2��6-4��4����8=10+1=11������
����ˮ��Ϊ11�����ף�
��3����4a-12��Ԫ��
��4����5�·ݲ�����6m3ʱ��ˮ��Ϊ��-6x+92��Ԫ��
��5�·ݳ���6m3ʱ��ˮ��Ϊ��-4x+80��Ԫ��


 ��ѧ��ʦ����ϵ�д�
��ѧ��ʦ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij����2014��Ͷ���������2 500��Ԫ��2016��Ͷ���������3025��Ԫ��
��1����2014����2016��õ���Ͷ��������ѵ���ƽ�������ʣ�
��2������(1)���õ���ƽ�������ʣ�Ԥ��2017��õ�����Ͷ��������Ѷ�����Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����й���x��һԪ���η����У����������ʵ�������ǣ�������
A. x2��1��0 B. x2��x��1��0
C. x2��2x��3��0 D. 4x2��4x��1��0
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������һ��һ�ƴ�С���ȵ�С�����壬ÿ��С������ĸ������Ϸֱ��������1��2��3��4��5��6.��ͬʱ����������С�����壬�����dz��ϵ�������ֱַ����һ����λ��.����ɫ������Ϊʮλ����ɫ������Ϊ��λ������ش���������.
��1����ֱ�д��һ����Ȼ�¼���һ���������¼�.
��2���õ�����λ�������ж��ٸ������и�λ��ʮλ��������ͬ���м�����
��3����д��һ������������һ������¼�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ͬѧ�糿�����ܲ��������Լ�������2ǧ����л��ң�����������1��5ǧ������ң�Ȼ����������4��5ǧ������ѧУ�����ص������밴Ҫ��������и�����
��1���������Ϊԭ�㣬���ķ���Ϊ��������1����λ���ȱ�ʾ1ǧ�ף����㻭�����ᣬ���������ϱ�ʾ�������л���Ҽ�ѧУ��λ�ü���λ�ñ�ʾ����������
��2��л��Ҿ�ѧУ��Զ��
��3�����һ�����˶���ǧ�ף�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С��Ͷ������һ�ֽ���Ϊÿ��20Ԫ�Ļ���̨�������۹����з��֣�ÿ��������y�����������۵���x��Ԫ��֮��Ĺ�ϵ�ɽ��ƵĿ���һ�κ�����![]() �������۹��������۵��۲����ڳɱ��ۣ���ÿ���������ڳɱ��۵�80%��
�������۹��������۵��۲����ڳɱ��ۣ���ÿ���������ڳɱ��۵�80%��
��1����С��ÿ�»������Ϊw��Ԫ������ÿ�»������w��Ԫ�������۵���x��Ԫ��֮��ĺ�����ϵʽ����ȷ���Ա���x��ȡֵ��Χ��
��2�������۵��۶�Ϊ����Ԫʱ��ÿ�¿ɻ���������ÿ�µ���������Ƕ��٣�
��3�����С����Ҫÿ�»�õ�����Ϊ2000Ԫ����ôС��ÿ�µijɱ���Ҫ����Ԫ�����ɱ������ۡ���������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ݵ�������ͳ�ƣ�ÿ��8��00��21��00���õ�ĸ߷��ڣ��������ʱ����21��00������8��00���õ�ĵ�ʱ�ڣ��������ʱ����Ϊ�˻�����������ì�ܣ�ij�е��������ڱ��³�ͳһ��װ����ȷ�ʱ����������õ�ʵ������ȷ�ʱ����������ߣ�������±���
ʱ�� | ����ǰ | ������ | |
��ʱ��8��00~21��00�� | ��ʱ��21��00~����8��00�� | ||
��� | ÿ��0��52Ԫ | ÿ��0��55Ԫ | ÿ��0��30Ԫ |
��1��С�ż���������ʱ���õ�50�ȣ�����ʱ���õ�20�ȣ������³�������������ڻ���ǰС�żҵĵ���������˻��Ǽ����ˣ����������˶���Ԫ����˵��������
��2��С�ż�������õ�95�ȣ�������Ȼ���ǰʹ��95�ȵ��ʡ��5��9Ԫ����С�ż������ʹ������ʱ����������ʱ�����ֱ��Ƕ��ٶȣ���12����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����20��ײˣ���ÿ��25ǧ��Ϊ�������������ǧ�����ֱ���������������ʾ����¼���£�

��1��20��ײ��У����ص�һ��������һ����ض���ǧ�ˣ�
��2����������Ƚϣ�20��ײ��ܼƳ����������ǧ�ˣ�
��3�����ײ�ÿǧ���ۼ�2.6Ԫ���������20��ײ˿�������Ԫ�����������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪����������![]() ��һ�κ���y=2x-1������һ�κ�����ͼ����a��b������a+1��b+k�����㡣
��һ�κ���y=2x-1������һ�κ�����ͼ����a��b������a+1��b+k�����㡣
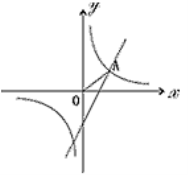
��1�����������Ľ���ʽ��
��2����ͼ����֪��A�ڵ�һ���ޣ���ͬʱ����������������ͼ���ϣ� ���A�����ꣻ
��3��������2���Ľ������������x�����Ƿ���ڵ�P��ʹ��AOPΪ���������Σ������ڣ��ѷ���������P�����궼��������������ڣ���˵�����ɡ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com