
【题目】在平面直角坐标系中,点O为原点,点A的坐标为(﹣8,0).如图1,正方形OBCD的顶点B在x轴的负半轴上,点C在第二象限.现将正方形OBCD绕点O顺时针旋转角α得到正方形OEFG.
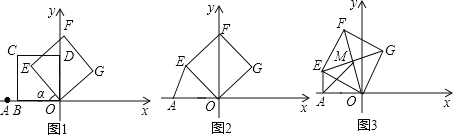
(1)如图2,若α=45°,OE=OA,求直线EF的函数表达式;
(2)如图3,若α为锐角,且tanα=![]() ,当EA⊥x轴时,正方形对角线EG与OF相交于点M,求线段AM的长;
,当EA⊥x轴时,正方形对角线EG与OF相交于点M,求线段AM的长;
(3)当正方形OEFG的顶点F落在y轴正半轴上时,直线AE与直线FG相交于点P,是否存在△OEP的两边之比为![]() :1?若存在,求出点P的坐标;若不存在,试说明理由.
:1?若存在,求出点P的坐标;若不存在,试说明理由.
【答案】(1)直线EF的解析式为y=x+8![]() ;(2)AM=6
;(2)AM=6![]() ;(3)满足条件的点P的坐标为(0,8),(﹣8,24),(﹣24,48).
;(3)满足条件的点P的坐标为(0,8),(﹣8,24),(﹣24,48).
【解析】
(1)过点E作EH⊥OA于点H,进而求出点E的坐标,再根据勾股定理求出OF的值,然后利用待定系数法,即可求出直线EF的解析式
(2)作MN⊥AM交x轴于点N,此时△AEM≌△NOM,得到AE=ON=4,△AMN是等腰直角三角形,即可求出AM的长;
(3)根据点F落在y轴正半轴上,通过改变正方形的边长,画出直线AE与直线FG相交的点P,并判断△OEP的其中两边之比能否为2:1,当△OEP的其中两边之比为![]() :1时,再通过分类讨论确定出图形,根据图形性质,利用勾股定理、相似三角形、三角函数等知识求得点P的坐标
:1时,再通过分类讨论确定出图形,根据图形性质,利用勾股定理、相似三角形、三角函数等知识求得点P的坐标
(1)∵OE=OA=8,α=45°,
∴E(﹣4![]() ,4
,4![]() ),F(0,8
),F(0,8![]() ),
),
设直线EF的解析式为y=kx+b,则有![]() ,
,
解得![]()
∴直线EF的解析式为y=x+8![]() .
.
(2)如图3中,作MH⊥OA于H,MK⊥AE交AE的延长线于K.
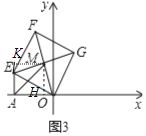
在Rt△AEO中,tan∠AOE=![]() ,OA=8,
,OA=8,
∴AE=4,
∵四边形EOGF是正方形,
∴∠EMO=90°,
∵∠EAO=∠EMO=90°,
∴E、A、O、M四点共圆,
∴∠EAM=∠EOM=45°,
∴∠MAK=∠MAH=45°,∵MK⊥AE,MH⊥OA,
∴MK=MH,四边形KAOM是正方形,
∵EM=OM,
∴△MKE≌△MHO,
∴EK=OH,
∴AK+AH=2AH=AE+EK+OA﹣OH=12,
∴AH=6,
∴AM=![]() AH=6
AH=6![]() .
.
(3)如图2中,设F(0,2a),则E(﹣a,a).
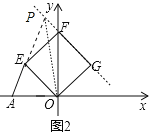
∵A(﹣8,0),E(﹣a,a),
∴直线AP的解析式为y=![]() ,直线FG的解析式为y=﹣x+2a,
,直线FG的解析式为y=﹣x+2a,
由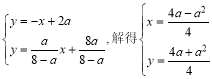 ,
,
∴P(![]() ).
).
①当PO=![]() OE时,∴PO2=2OE2,
OE时,∴PO2=2OE2,
则有:![]() =4a2,
=4a2,
解得a=4或﹣4(舍弃)或0(舍弃),
此时P(0,8).
②当PO=![]() PE时,则有:
PE时,则有:![]() =2[(
=2[(![]() )2],
)2],
解得:a=4或12,
此时P(0,8)或(﹣24,48),
③当PE=![]() EO时,[(
EO时,[(![]() )2]=4a2,
)2]=4a2,
解得a=8或0(舍弃),
∴P(﹣8,24)
综上所述,满足条件的点P的坐标为(0,8),(﹣8,24),(﹣24,48).


 智慧小复习系列答案
智慧小复习系列答案科目:初中数学 来源: 题型:
【题目】如图,直线y=kx+b与双曲线![]() (x﹤0)相交于A(-4,a)、B(-1,4)两点.
(x﹤0)相交于A(-4,a)、B(-1,4)两点.

(1)求直线和双曲线的解析式;
(2)在y轴上存在一点P,使得PA+PB的值最小,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】七巧板是我们祖先的一项卓越创造,被西方人誉为“东方魔板”.下面的两幅图正方形(如图1)、“风车型”(如图2)都是由同一副七巧板拼成的,则图中正方形ABCD,EFGH的面积比为______.
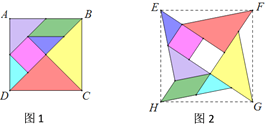
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,甲、乙两船同时由港口A出发开往海岛B,甲船沿东北方向向海岛B航行,其速度为15海里/小时;乙船速度为20海里/小时,先沿正东方向航行1小时后,到达C港口接旅客,停留半小时后再转向北偏东30°方向开往B岛,其速度仍为20海里/小时.
(1)求港口A到海岛B的距离;
(2)B岛建有一座灯塔,在离灯塔方圆5海里内都可以看见灯塔,问甲、乙两船哪一艘先看到灯塔?
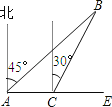
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BD是△ABC的角平分线,点E,F分别在BC,AB上,且DE∥AB,BE=AF.
(1)求证:四边形ADEF是平行四边形;
(2)若∠ABC=60°,BD=6,求DE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AE平分∠BAC,BE⊥AE于点E,点F是BC的中点.
(1)如图1,BE的延长线与AC边相交于点D,求证:EF=![]() (AC﹣AB);
(AC﹣AB);
(2)如图2,请直接写出线段AB、AC、EF之间的数量关系。
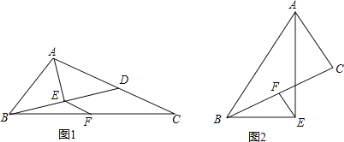
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若二次函数![]() 的图象与
的图象与![]() 轴分别交于点
轴分别交于点![]() 、
、![]() ,且过点
,且过点![]() .
.
(1)求二次函数表达式;
(2)若点![]() 为抛物线上第一象限内的点,且
为抛物线上第一象限内的点,且![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)在抛物线上(![]() 下方)是否存在点
下方)是否存在点![]() ,使
,使![]() ?若存在,求出点
?若存在,求出点![]() 到
到![]() 轴的距离;若不存在,请说明理由.
轴的距离;若不存在,请说明理由.
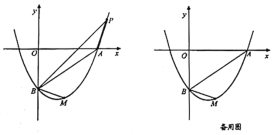
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y1=kx+b(k≠0)与反比例函数![]() (m≠0)的图象交于点A(﹣1,6),B(a,﹣2).
(m≠0)的图象交于点A(﹣1,6),B(a,﹣2).
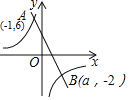
(1)求一次函数与反比例函数的解析式;
(2)根据函数图象,直接写出不等式![]() 的解集.
的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场购进甲、乙两种商品,甲种商品共用了2000元,乙种商品共用了2400元![]() 已知乙种商品每件进价比甲种商品每件进价多8元,且购进的甲、乙两种商品件数相同.
已知乙种商品每件进价比甲种商品每件进价多8元,且购进的甲、乙两种商品件数相同.
![]() 求甲、乙两种商品的每件进价;
求甲、乙两种商品的每件进价;
![]() 该商场将购进的甲、乙两种商品进行销售,甲种商品的销售单价为60元,乙种商品的销售单价为88元,销售过程中发现甲种商品销量不好,商场决定:甲种商品销售一定数量后,将剩余的甲种商品按原销售单价的七折销售;乙种商品销售单价保持不变
该商场将购进的甲、乙两种商品进行销售,甲种商品的销售单价为60元,乙种商品的销售单价为88元,销售过程中发现甲种商品销量不好,商场决定:甲种商品销售一定数量后,将剩余的甲种商品按原销售单价的七折销售;乙种商品销售单价保持不变![]() 要使两种商品全部售完后共获利不少于2460元,问甲种商品按原销售单价至少销售多少件?
要使两种商品全部售完后共获利不少于2460元,问甲种商品按原销售单价至少销售多少件?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com