
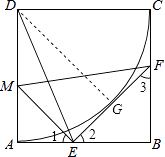
【题目】如图,在边长为2的正方形ABCD中,以点D为圆心、DC为半径作 ![]() ,点E在AB上,且与A、B两点均不重合,点M在AD上,且ME=MD,过点E作EF⊥ME,交BC于点F,连接DE、MF.
,点E在AB上,且与A、B两点均不重合,点M在AD上,且ME=MD,过点E作EF⊥ME,交BC于点F,连接DE、MF.
(1)求证:EF是 ![]() 所在⊙D的切线;
所在⊙D的切线;
(2)当MA= ![]() 时,求MF的长;
时,求MF的长;
(3)试探究:△MFE能否是等腰直角三角形?若是,请直接写出MF的长度;若不是,请说明理由.
【答案】
(1)
证明:过点D作DG⊥EF于G,
∵ME=MD,
∴∠MDE=∠MED,
∵EF⊥ME,
∴∠DEM+∠GED=90°,
∵∠DAB=90°,
∴∠MDE+∠AED=90°,
∴∠AED=∠GED,
∵在△ADE和△GDE中,
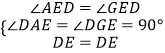 ,
,
∴△ADE≌△GDE(AAS),
∴AD=GD,
∵ ![]() 的半径为DC,即AD的长度,
的半径为DC,即AD的长度,
∴EF是 ![]() 所在⊙D的切线;
所在⊙D的切线;
(2)
MA= ![]() 时,ME=MD=2﹣
时,ME=MD=2﹣ ![]() =
= ![]() ,
,
在Rt△AME中,AE= ![]() =
= ![]() =1,
=1,
∴BE=AB﹣AE=2﹣1=1,
∵EF⊥ME,
∴∠1+∠2=180°﹣90°=90°,
∵∠B=90°,
∴∠2+∠3=90°,
∴∠1=∠3,
又∵∠DAB=∠B=90°,
∴△AME∽△BEF,
∴ ![]() ,
,
即 ![]() ,
,
解得EF= ![]() ,
,
在Rt△MEF中,MF= ![]() ;
;
(3)
假设△MFE能是等腰直角三角形,
则ME=EF,
∵在△AME和△BEF中,
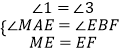 ,
,
∴△AME≌△BEF(AAS),
∴MA=BE,
设AM=BE=x,
则MD=AD﹣MA=2﹣x,AE=AB﹣BE=2﹣x,
∵ME=MD,
∴ME=2﹣x,
∴ME=AE,
∵ME、AE分别是Rt△AME的斜边与直角边,
∴ME≠AE,
∴假设不成立,
故△MFE不能是等腰直角三角形.
【解析】(1)过点D作DG⊥EF于G,根据等边对等角可得∠MDE=∠MED,然后根据等角的余角相等求出∠AED=∠GED,再利用“角角边”证明△ADE和△GDE全等,根据全等三角形对应边相等可得AD=GD,再根据切线的定义即可得证;(2)求出ME=MD= ![]() ,然后利用勾股定理列式求出AE,再求出BE,根据同角的余角相等求出∠1=∠3,然后求出△AME和△BEF相似,根据相似三角形对应边成比例列式求出EF,再利用勾股定理列式计算即可得解;(3)假设△MFE能是等腰直角三角形,根据等腰直角三角形的性质可得ME=EF,先利用“角角边”证明△AME和△BEF全等,根据全等三角形对边角相等可得AM=BE,设AM=BE=x,然后表示出MD,AE,再根据ME=MD,从而得到ME=AE,根据直角三角形斜边大于直角边可知△MEF不可能是等腰直角三角形.
,然后利用勾股定理列式求出AE,再求出BE,根据同角的余角相等求出∠1=∠3,然后求出△AME和△BEF相似,根据相似三角形对应边成比例列式求出EF,再利用勾股定理列式计算即可得解;(3)假设△MFE能是等腰直角三角形,根据等腰直角三角形的性质可得ME=EF,先利用“角角边”证明△AME和△BEF全等,根据全等三角形对边角相等可得AM=BE,设AM=BE=x,然后表示出MD,AE,再根据ME=MD,从而得到ME=AE,根据直角三角形斜边大于直角边可知△MEF不可能是等腰直角三角形.


 百年学典课时学练测系列答案
百年学典课时学练测系列答案科目:初中数学 来源: 题型:
【题目】我们定义三个有理数之间的新运算法则“⊕”:a⊕b⊕c=![]() (|a﹣b﹣c|+a+b+c),如:1⊕(﹣2)⊕3=
(|a﹣b﹣c|+a+b+c),如:1⊕(﹣2)⊕3=![]() [|1﹣(﹣2)﹣3|+1+(﹣2)+3]=l,在﹣2,﹣4,﹣5,0,2,5,6这7个数中,任意取三个数作为a,b,c的值,进行“a⊕b⊕c“运算,求在所有计算的结果中的最大值是_____.
[|1﹣(﹣2)﹣3|+1+(﹣2)+3]=l,在﹣2,﹣4,﹣5,0,2,5,6这7个数中,任意取三个数作为a,b,c的值,进行“a⊕b⊕c“运算,求在所有计算的结果中的最大值是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角梯形ABCD中,AB=2,BC=4,AD=6,M是CD的中点,点P在直角梯形的边上沿A→B→C→M运动,则△APM的面积y与点P经过的路程x之间的函数关系用图象表示是( )
A.
B.
C.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线a∥b,直线c与a、b都相交,从所标识的∠1、∠2、∠3、∠4、∠5这五个角中任意选取两个角,则所选取的两个角互为补角的概率是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(﹣4,3)、B(﹣3,1)、C(﹣1,3).
(1)请按下列要求画图:
①将△ABC先向右平移4个单位长度、再向上平移2个单位长度,得到△A1B1C1 , 画出△A1B1C1;
②△A2B2C2与△ABC关于原点O成中心对称,画出△A2B2C2 .
(2)在(1)中所得的△A1B1C1和△A2B2C2关于点M成中心对称,请直接写出对称中心M点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】自古以来,钓鱼岛及其附属岛屿都是我国固有领土.如图,为了开发利用海洋资源,我勘测飞机测量钓鱼岛附属岛屿之一的北小岛(又称为鸟岛)两侧端点A、B的距离,飞机在距海平面垂直高度为100米的点C处测得端点A的俯角为60°,然后沿着平行于AB的方向水平飞行了800米,在点D测得端点B的俯角为45°,求北小岛两侧端点A、B的距离.
(结果精确到0.1米,参考数 ![]() ≈1.73,
≈1.73, ![]() ≈1.41)
≈1.41)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线l:y= ![]() x+1交x轴于点A,交y轴于点B,点A1、A2、A3 , …在x轴上,点B1、B2、B3 , …在直线l上.若△OB1A1 , △A1B2A2 , △A2B3A3 , …均为等边三角形,则△A5B6A6的周长是( )
x+1交x轴于点A,交y轴于点B,点A1、A2、A3 , …在x轴上,点B1、B2、B3 , …在直线l上.若△OB1A1 , △A1B2A2 , △A2B3A3 , …均为等边三角形,则△A5B6A6的周长是( )
A.24 ![]()
B.48 ![]()
C.96 ![]()
D.192 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图:∠1=∠2,∠3+∠4= 180°;确定直线a,c的位置关系,并说明理由;
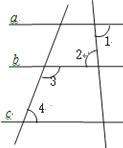
解:a c;
理由:∵∠1=∠2( ),
∴ a // ( );
∵ ∠3+∠4= 180°( ),
∴ c // ( );
∵ a // ,c // ,
∴ // ( );
查看答案和解析>>
科目:初中数学 来源: 题型:
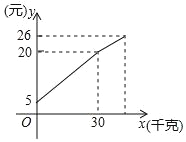
【题目】王大爷带了若干千克自产的土豆进城出售,为了方便,他带了一些零钱备用,按市场价出售一些后,又降价出售,售出土豆的千克数x与他手中持有的钱数y(含备用零钱)的关系如图所示.根据图象回答下列问题:
(1)王大爷自带的零钱是多少?
(2)降价前他每千克土豆出售的价格是多少?
(3)降价后他按每千克0.4元将剩余土豆售完,这时他手中的钱(含备用零钱)是26元,问他一共带了多少千克土豆?
(4)写出售出土豆的千克数x与他手中持有的钱数y(含备用零钱)的关系式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com