
����Ŀ���Թ����������㵺���丽�����춼���ҹ�������������ͼ��Ϊ�˿������ú�����Դ���ҿ���ɻ��������㵺��������֮һ�ı�С�����ֳ�Ϊ������˵�A��B�ľ��룬�ɻ��ھຣƽ�洹ֱ�߶�Ϊ100�ĵ�C����ö˵�A�ĸ���Ϊ60�㣬Ȼ������ƽ����AB�ķ���ˮƽ������800�ף��ڵ�D��ö˵�B�ĸ���Ϊ45�㣬��С������˵�A��B�ľ��룮
�������ȷ��0.1�ף��ο��� ![]() ��1.73��
��1.73�� ![]() ��1.41��
��1.41��
���𰸡��⣺����A��AE��CD�ڵ�E������B��BF��CD�ڵ�F��
��AB��CD��
���AEF=��EFB=��ABF=90�㣬
���ı���ABFEΪ���Σ�
��AB=EF��AE=BF��
�������֪��AE=BF=100�ף�CD=800�ף�
��Rt��AEC�У���C=60�㣬AE=100�ף�
��CE= ![]() ���ף���
���ף���
��Rt��BFD�У���BDF=45�㣬BF=100��
��DF= ![]() =100���ף���
=100���ף���
��AB=EF=CD+DF��CE=800+100�� ![]() ��900��
��900�� ![]() ��1.73��900��57.67��842.3�ף�
��1.73��900��57.67��842.3�ף�
�𣺵�������˵�A��B�ľ���ԼΪ842.3�ף�
�����������ȹ���A��AE��CD�ڵ�E������B��BF��CD�ڵ�F�����ı���ABFEΪ���Σ����ݾ��ε����ʣ��ɵ�AB=EF��AE=BF���������֪��AE=BF=100�ף�CD=800�ף�Ȼ��ֱ���Rt��AEC��Rt��BFD�У��������Ǻ����������CE��DF�ij����̶���õ�������A��B�ľ��룮
�����㾫����������Ĺؼ����������ֱ�������ε����֪ʶ��������ֱ�������ε����ݣ��ٱߵĹ�ϵa2+b2=c2���ڽǵĹ�ϵ��A+B=90�㣻�۱߽ǹ�ϵ�����Ǻ����Ķ��壮(ע�⣺��������ʹ���м����ݺͳ���)���Լ��Թ������Ǹ�����������⣬�˽����ǣ�������ˮƽ���Ϸ��Ľǣ����ǣ�������ˮƽ���·��Ľǣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ����ֱ�Ĺ�·����A��B���أ��������г���A�ص�B�أ��������г���B�ص�A�أ�����A�غ�������ԭ·���أ���ͼ�Ǽס���������B�صľ���y��km������ʻʱx��h��֮��ĺ���ͼ����ͼ�����������⣺ 
��1��д��A��B����֮��ľ��룻
��2�������M�����꣬�����õ���������ʾ��ʵ�����壻
��3��������֮�䱣�ֵľ��벻����3kmʱ���ܹ������߶Խ���������ϵ����ֱ��д���ס��������ܹ������߶Խ���������ϵʱx��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��1������Rt��ABC����ACB=90�㣬�ֱ���AB��BCΪһ��������������ABFG��BCED������AD��CF��AD��CF���ڵ�M��
��1����֤����ABD�ա�FBC��
��2����ͼ��2������֪AD=6�����ı���AFDC�������
��3���ڡ�ABC�У���BC=a��AC=b��AB=c������ACB��90��ʱ��c2��a2+b2 �� �������ABC�У�c2=a2+b2+k����a=3��b=2�����Σ�̽��k��ȡֵ��Χ��ֻ��д����õ��Ľ��ۼ��ɣ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У�������P��������y=ax2�ϣ���P�����F��0��n��������ֱ��y=��nʼ�ձ������У���n=���ú�a�Ĵ���ʽ��ʾ����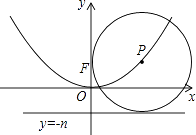
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڱ߳�Ϊ2��������ABCD�У��Ե�DΪԲ�ġ�DCΪ�뾶�� ![]() ����E��AB�ϣ�����A��B��������غϣ���M��AD�ϣ���ME=MD������E��EF��ME����BC�ڵ�F������DE��MF��
����E��AB�ϣ�����A��B��������غϣ���M��AD�ϣ���ME=MD������E��EF��ME����BC�ڵ�F������DE��MF��
��1����֤��EF�� ![]() ���ڡ�D�����ߣ�
���ڡ�D�����ߣ�
��2����MA= ![]() ʱ����MF�ij���
ʱ����MF�ij���
��3����̽������MFE�ܷ��ǵ���ֱ�������Σ����ǣ���ֱ��д��MF�ij��ȣ������ǣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ���ı���ABCD�У�AB��BC�������²�����ͼ����AΪԲ�ģ�С��AD�ij�Ϊ�뾶�������ֱ�AB��CD��E��F���ٷֱ���E��FΪԲ�ģ����� ![]() EF�ij��뾶�������������ڵ�G��������AG��CD�ڵ�H�������н��ۣ���AGƽ�֡�DAB����CH=
EF�ij��뾶�������������ڵ�G��������AG��CD�ڵ�H�������н��ۣ���AGƽ�֡�DAB����CH= ![]() DH���ۡ�ADH�ǵ��������Σ���S��ADH=
DH���ۡ�ADH�ǵ��������Σ���S��ADH= ![]() S�ı���ABCH ��
S�ı���ABCH ��
������ȷ���У� ��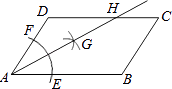
A.�٢ڢ�
B.�٢ۢ�
C.�ڢ�
D.�٢�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڵ�������ABCD�У�DC��AB��E��DC�ӳ����ϵĵ㣬����AE����BC�ڵ�F��
��1����֤����ABF�ס�ECF��
��2�����AD=5cm��AB=8cm��CF=2cm����CE�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��AOB�У���AOBΪֱ�ǣ�A����3��a����B��3��b����a+b��12=0�����AOB�����Ϊ_____��
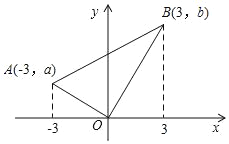
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У���C=90�㣬��B=60�㣬D��AC��һ�㣬DE��AB��E����CD=2��DE=1����BC�ij�Ϊ�� ��
A.2
B.![]()
C.2 ![]()
D.4 ![]()
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com