
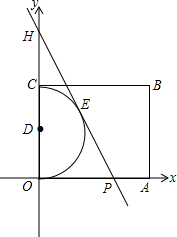 如图,在直角坐标系中,半圆直径为OC,半圆圆心D的坐标为(0,2),四边形OABC是矩形,∠OPH=60°.半圆D的切线PH分别与x轴和y轴相交于点P与点H,切点为点E.
如图,在直角坐标系中,半圆直径为OC,半圆圆心D的坐标为(0,2),四边形OABC是矩形,∠OPH=60°.半圆D的切线PH分别与x轴和y轴相交于点P与点H,切点为点E.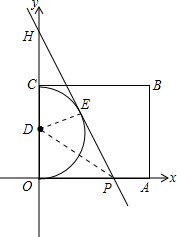
| 1 |
| 2 |
| DP2-OD2 |
| 3 |
| 3 |
| PH2-OP2 |
| 3 |
|
|
| 3 |
|
| 1 |
| 2 |
| 3 |
| 120×π×22 |
| 360 |
| 3 |
| 4π |
| 3 |


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
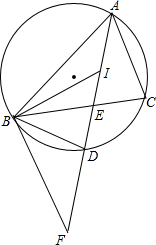 如图,点I是△ABC的内心,线段AI的延长线交△ABC的外接圆于点D、BC于点E.
如图,点I是△ABC的内心,线段AI的延长线交△ABC的外接圆于点D、BC于点E.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,公园内有一颗景观树,AB的影子请好落在地图BC和地图CD上,经测量CD=4m,BC=10m,已知该坡面CD与地面成30°角,且此时测得2m的竹竿的影子是1m,求这颗景观树的高度.
如图,公园内有一颗景观树,AB的影子请好落在地图BC和地图CD上,经测量CD=4m,BC=10m,已知该坡面CD与地面成30°角,且此时测得2m的竹竿的影子是1m,求这颗景观树的高度.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com