
分析 (1)先变形得到(x-1)2=2,然后利用直接开平方法解方程;
(2)先利用配方法得到(x-2)2=3,然后利用直接开平方法解方程;
(3)先计算判别式的值,然后根据判别式的意义判断方程无实数解;
(4)利用因式分解法解方程.
解答 解:(1)(x-1)2=2,
x-1=±$\sqrt{2}$,
所以x1=1+$\sqrt{2}$,x2=1-$\sqrt{2}$;
(2)x2-4x+4=3,
(x-2)2=3,
x-2=±$\sqrt{3}$,
所以x1=2+$\sqrt{3}$,x2=2-$\sqrt{3}$;
(3)△=(-8)2-4×17<0,
所以方程没有实数解;
(4)(x-2)(x+1)=0,
x-2=0或x+1=0,
所以x1=2,x2=-1.
点评 本题考查了解一元二次方程-因式分解法:先把方程的右边化为0,再把左边通过因式分解化为两个一次因式的积的形式,那么这两个因式的值就都有可能为0,这就能得到两个一元一次方程的解,这样也就把原方程进行了降次,把解一元二次方程转化为解一元一次方程的问题了(数学转化思想).也考查了直接开平方法和配方法解一元二次方程.


科目:初中数学 来源: 题型:解答题
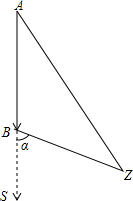 我渔政巡逻艇在A处测得距钓鱼岛Z的距离140海里,向南直行到B出测得距钓鱼岛Z的距离100海里,此时测得直行方向与钓鱼岛Z方向夹角为α,如图所示.求渔政巡逻艇行驶路程AB是多少海里?(sinα=$\frac{{\sqrt{3}}}{2}$,cosα=$\frac{1}{2}$,tanα=$\sqrt{3}$).
我渔政巡逻艇在A处测得距钓鱼岛Z的距离140海里,向南直行到B出测得距钓鱼岛Z的距离100海里,此时测得直行方向与钓鱼岛Z方向夹角为α,如图所示.求渔政巡逻艇行驶路程AB是多少海里?(sinα=$\frac{{\sqrt{3}}}{2}$,cosα=$\frac{1}{2}$,tanα=$\sqrt{3}$).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{x}{3}$=$\frac{y}{4}$ | B. | $\frac{x+4}{4}$=$\frac{y+3}{3}$ | C. | $\frac{x+y}{4+3}$=$\frac{x}{4}$ | D. | $\frac{4-x}{x}$=$\frac{3-y}{y}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,反比例函数y=$\frac{k}{x}$的图象经过矩形AOBC的边AC的中点E,与另一边BC交于点D,连接DE,若S△ECD=2,则k的值为( )
如图,反比例函数y=$\frac{k}{x}$的图象经过矩形AOBC的边AC的中点E,与另一边BC交于点D,连接DE,若S△ECD=2,则k的值为( )| A. | 2 | B. | 4 | C. | 8 | D. | 16 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
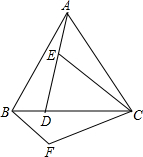 如图,已知△ABC是正三角形,点D是边BC上一点,连接AD,点E是线段AD上一点,连接CE,点F是△ABC外一点,∠CAD=∠CBF,连接BF和CF.
如图,已知△ABC是正三角形,点D是边BC上一点,连接AD,点E是线段AD上一点,连接CE,点F是△ABC外一点,∠CAD=∠CBF,连接BF和CF.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com