
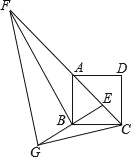
【题目】在正方形ABCD中,对角线AC上取一点E,连接BE,过B作BE的垂线交CA的延长线于F,垂足为B,将△BEF沿BF翻折得到△BGF,连接GC.若tan∠EFG=![]() ,
,![]() ,则GC=_____.
,则GC=_____.
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC的周长是20,OB和OC分别平分∠ABC和∠ACB,OD⊥BC于点D,且OD=3,则△ABC的面积是( )

A. 20 B. 25 C. 30 D. 35
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】4月23日为“世界读书日”,每年的这一天,世界100多个国家都会举办各种各样的庆祝和图书宣传活动.我县某书店借此机会决定开展“读书节”活动,为迎接“读书节”制定了活动计划.以下是活动计划书的部分信息:
“读书节”活动计划书 | ||
图书类別 | A类 | B类 |
进价(元/本) | 18 | 12 |
备注 | (1)用不超过16800元购进A、B两类图书共1000本: (2)A类图书不少于600本: | |
(1)陈经理査看计划书时发现:A类图书的标价是B类图书标价的1.5倍,若顾客同样用540元购买图书,能购买A类图书数量比B类图书的数量少10本,请求出A、B两类图书的标价;
(2)经市场调查后,陈经理发现它们高估了“读书节”对图书销售的影响:便调整了销售方案;A类图书每本按标价降低2元销售,B类图书价格不变,那么该书店应如何进货才能获得最大利润?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,已知直线y=-2x+4与x轴、y轴分别交于点A、C,以OA、OC为边在第一象限内作长方形OABC.

(1)求点A、C的坐标;
(2)将△ABC对折,使得点A的与点C重合,折痕交AB于点D,求直线CD的解析式(图②);
(3)在坐标平面内,是否存在点P(除点B外),使得△APC与△ABC全等?若存在,请直接写出所有符合条件的点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《函数的图象与性质》拓展学习片段展示:
【问题】
如图①,在平面直角坐标系中,抛物线y=a(x-2)2-4经过原点O,与x轴的另一个交点为A,则a= ,点A的坐标为 .
【操作】
将图①中的抛物线在x轴下方的部分沿x轴翻折到x轴上方,如图②.直接写出翻折后的这部分抛物线对应的函数解析式: .
【探究】
在图②中,翻折后的这部分图象与原抛物线剩余部分的图象组成了一个“W”形状的新图象,则新图象对应的函数y随x的增大而增大时,x的取值范围是 .
【应用】结合上面的操作与探究,继续思考:
如图③,若抛物线y=(x-h)2-4与x轴交于A,B两点(A在B左),将抛物线在x轴下方的部分沿x轴翻折,同样,也得到了一个“W”形状的新图象.
(1)求A、B两点的坐标;(用含h的式子表示)
(2)当1<x<2时,若新图象的函数值y随x的增大而增大,求h的取值范围.



查看答案和解析>>
科目:初中数学 来源: 题型:
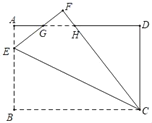
【题目】如图,长方形纸片ABCD中,AB=4,BC=6,点E在AB边上,将纸片沿CE折叠,点B落在点F处,EF,CF分别交AD于点G,H,且EG=GH,则AE的长为( )
A. ![]() B. 1C.
B. 1C. ![]() D. 2
D. 2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)已知⊙O的直径为10cm,点A为⊙O外一定点,OA=12cm,点P为⊙O上一动点,求PA的最大值和最小值.
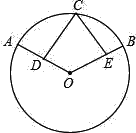
(2)如图:![]() =
=![]() ,D、E分别是半径OA和OB的中点.求证:CD=CE.
,D、E分别是半径OA和OB的中点.求证:CD=CE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数y=x-5,令x=![]() ,1,
,1,![]() ,2,
,2,![]() ,3,
,3,![]() ,4,
,4,![]() ,5,可得函数图象上的十个点.在这十个点中随机取两个点P(x1,y1),Q(x2,y2),则P,Q两点在同一反比例函数图象上的概率是( )
,5,可得函数图象上的十个点.在这十个点中随机取两个点P(x1,y1),Q(x2,y2),则P,Q两点在同一反比例函数图象上的概率是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com