
【题目】使得函数值为零的自变量的值称为函数的零点。例如,对于函数![]() ,令y=0,可得x=1,我们就说1是函数
,令y=0,可得x=1,我们就说1是函数![]() 的零点。
的零点。
己知函数![]() (
(![]() m为常数)。
m为常数)。
(1)当![]() =0时,求该函数的零点;
=0时,求该函数的零点;
(2)证明:无论![]() 取何值,该函数总有两个零点;
取何值,该函数总有两个零点;
(3)设函数的两个零点分别为![]() 和
和![]() ,且
,且![]() ,此时函数图象与x轴的交点分
,此时函数图象与x轴的交点分
别为A、B(点A在点B左侧),点M在直线![]() 上,当MA+MB最小时,求直线AM的函数解析式。
上,当MA+MB最小时,求直线AM的函数解析式。
【答案】(1)当![]() =0时,该函数的零点为
=0时,该函数的零点为![]() 和
和![]() 。
。
(2)见解析,
(3)AM的解析式为![]() 。
。
【解析】
(1)根据题中给出的函数的零点的定义,将m=0代入y=x2-2mx-2(m+3),然后令y=0即可解得函数的零点;
(2)令y=0,函数变为一元二次方程,要想证明方程有两个解,只需证明△>0即可;
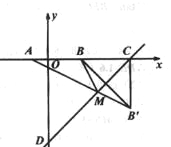
(3)根据题中条件求出函数解析式进而求得A、B两点坐标,个、作点B关于直线y=x-10的对称点B′,连接AB′,求出点B′的坐标即可求得当MA+MB最小时,直线AM的函数解析式
(1)当![]() =0时,该函数的零点为
=0时,该函数的零点为![]() 和
和![]() 。
。
(2)令y=0,得△=![]()
∴无论![]() 取何值,方程
取何值,方程![]() 总有两个不相等的实数根。
总有两个不相等的实数根。
即无论![]() 取何值,该函数总有两个零点。
取何值,该函数总有两个零点。
(3)依题意有![]() ,
,![]()
由![]() 解得
解得![]() 。
。
∴函数的解析式为![]() 。
。
令y=0,解得![]()
∴A(![]() ),B(4,0)
),B(4,0)
作点B关于直线![]() 的对称点B’,连结AB’,
的对称点B’,连结AB’,
则AB’与直线![]() 的交点就是满足条件的M点。
的交点就是满足条件的M点。
易求得直线![]() 与x轴、y轴的交点分别为C(10,0),D(0,10)。
与x轴、y轴的交点分别为C(10,0),D(0,10)。
连结CB’,则∠BCD=45°
∴BC=CB’=6,∠B’CD=∠BCD=45°
∴∠BCB’=90°
即B’(![]() )
)
设直线AB’的解析式为![]() ,则
,则
![]() ,解得
,解得![]()
∴直线AB’的解析式为![]() ,
,
即AM的解析式为![]() 。
。


科目:初中数学 来源: 题型:
【题目】某品牌牛奶供应商提供A,B,C,D四种不同口味的牛奶供学生饮用.某校为了了解学生对不同口味的牛奶的喜好,对全校订牛奶的学生进行了随机调查,并根据调查结果绘制了如下两幅不完整的统计图.根据统计图的信息解决下列问题:

(1)本次调查的学生有多少人?
(2)补全上面的条形统计图;
(3)扇形统计图中C对应的中心角度数是_____;
(4)若该校有600名学生订了该品牌的牛奶,每名学生每天只订一盒牛奶,要使学生能喝到自己喜欢的牛奶,则该牛奶供应商送往该校的牛奶中,A,B口味的牛奶共约多少盒?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 地和
地和![]() 地之间的铁路交通设有特快列车和普通列车两种车次,某天一辆普通列车从A地出发匀速驶向
地之间的铁路交通设有特快列车和普通列车两种车次,某天一辆普通列车从A地出发匀速驶向![]() 地,同时另一辆特快列车从
地,同时另一辆特快列车从![]() 地出发匀速驶向
地出发匀速驶向![]() 地,两车与
地,两车与![]() 地的距离
地的距离![]() (千米)与行驶时间
(千米)与行驶时间![]() (时)的函数关系如图所示.
(时)的函数关系如图所示.

(1)![]() 地到
地到![]() 地的距离为 千米,普通列车到达
地的距离为 千米,普通列车到达![]() 地所用时间为 小时;
地所用时间为 小时;
(2)求特快列车与![]() 地的距离
地的距离![]() 与
与![]() 的函数关系式;
的函数关系式;
(3)在![]() 、
、![]() 两地之间有一座铁路桥,特快列车到铁路桥后又行驶
两地之间有一座铁路桥,特快列车到铁路桥后又行驶![]() 小时与普通列车相遇,直接写出
小时与普通列车相遇,直接写出![]() 地与铁路桥之间的距离 .
地与铁路桥之间的距离 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,D、E分别是AB、AC边上的点,点F在BC的延长线上,DE∥BC,若∠A=48°,∠1=54°,则下列正确的是( )

A. ∠2=48°B. ∠2=54°C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=﹣![]() x+4与x轴、y轴分别交于点A、B、C是线段AB上一点,四边形OADC是菱形,则OD的长为( )
x+4与x轴、y轴分别交于点A、B、C是线段AB上一点,四边形OADC是菱形,则OD的长为( )
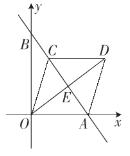
A. 4.2B. 4.8C. 5.4D. 6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,某海盗船以20海里/小时的速度在某海域执行巡航任务,当海监船由西向东航行至A处使,测得岛屿P恰好在其正北方向,继续向东航行1小时到达B处,测得岛屿P在其北偏西30°方向,保持航向不变又航行2小时到达C处,求出此时海监船与岛屿P之间的距离(即PC的长,结果精确到0.1)(参考数据:![]() ≈1.732,
≈1.732,![]() ≈1.414)
≈1.414)
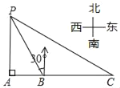
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形纸片ABCD中,∠A=60°,折叠菱形纸片ABCD,使点C落在DP(P为AB中点)所在的直线上,得到经过点D的折痕DE,则∠DEC的大小为( )

A. 78° B. 45° C. 60° D. 75°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数![]() 的图象与
的图象与![]() 轴交于点
轴交于点![]() ,对称轴为直线
,对称轴为直线![]() ,
,![]() ,下列结论:①
,下列结论:①![]() ;②9a+3b+c=0;③若点
;②9a+3b+c=0;③若点![]() ,点
,点![]() 是此函数图象上的两点,则
是此函数图象上的两点,则![]() ;④
;④![]() .其中正确的个数( )
.其中正确的个数( )
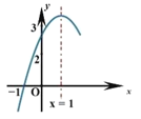
A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某无人机于空中![]() 处探测到目标
处探测到目标![]() 的俯角分别是
的俯角分别是![]() ,此时无人机的飞行高度
,此时无人机的飞行高度![]() 为
为![]() ,随后无人机从
,随后无人机从![]() 处继续水平飞行
处继续水平飞行![]() m到达
m到达![]() 处.
处.
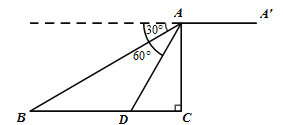
(1)求![]() 之间的距离
之间的距离
(2)求从无人机![]() 上看目标
上看目标![]() 的俯角的正切值.
的俯角的正切值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com