
����Ŀ����ͼ���ڡ�ABC�У�AB��AC��10cm��BD��AC�ڵ�D��BD��8cm����M�ӵ�A��������AC�ķ��������˶���ͬʱֱ��PQ�ɵ�B��������BA�ķ��������˶����˶�������ʼ�ձ���PQ��AC��ֱ��PQ��AB�ڵ�P����BC�ڵ�Q����BD�ڵ�F������PM�����˶�ʱ��Ϊt�루0��t��5�����߶�CM�ij��ȼ���y�����߶�BP�ij��ȼ���y����y����y������ʱ��t�ĺ����仯�����ͼ��ʾ��
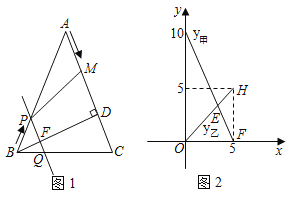
��1����ͼ2��֪����M���˶��ٶ���ÿ���� cm����t���� ��ʱ���ı���PQCM��ƽ���ı��Σ���ͼ2�з�ӳ��һ����ĵ����� ����д���˵�����꣩��
��2�����ı���PQCM�����Ϊycm2����y��t֮��ĺ�����ϵʽ��
��3������PC���Ƿ����ijһʱ��t��ʹ��M���߶�PC�Ĵ�ֱƽ�����ϣ������ڣ������ʱt��ֵ���������ڣ�˵�����ɣ�
���𰸡���1��2��![]() ��E��
��E��![]() ��
��![]() ������2��y��
������2��y��![]() t2��8t+40����3�����ڣ�t��
t2��8t+40����3�����ڣ�t��![]() sʱ����M���߶�PC�Ĵ�ֱƽ�����ϣ�
sʱ����M���߶�PC�Ĵ�ֱƽ�����ϣ�
��������
��1������ͼ2�жϳ���M���ٶ�Ϊ2cm/s��PQ���˶��ٶ�Ϊ1cm/s�������ı���PQCMΪƽ���ı��Σ�����ƽ���ı��ε����ʵõ��Ա�ƽ�У������õ�AP=AM���г�����t�ķ��̣�������̵Ľ�õ���������t��ֵ��
��2������PQ��AC�ɵ���PBQ�ס�ABC���������������ε���״��Ȼ��ͬ��֪��BPQҲΪ���������Σ���BP=PQ=t�����ú�t�Ĵ���ʽ�Ϳ��Ա�ʾ��BF�������õ����εĸ�PE=DF=8-t���ֵ�M���˶��ٶȺ�ʱ���֪��M�߹���·��AM=2t���������ε��µ�CM=10-2t�����������ε������ʽ���ɵõ�y��t�Ĺ�ϵʽ��
��3��������ڣ�����ݴ�ֱƽ�����ϵĵ㵽�߶����˵�ľ�����ȼ��ɵõ�MP=MC������M��MH��ֱAB����һ�Թ����ǵ���Ⱥ�һ��ֱ�ǵ���ȼ��ɵõ���AHM�ס�ADB�������Ƶõ���Ӧ�߳ɱ��������ú�t�Ĵ���ʽ��ʾ��AH��HM�ij�������AP�ij���AH�ij���ʾ��PH�ij����Ӷ���ֱ��������PHM�и��ݹ��ɶ�����ʾ��MP��ƽ��������AC�ij���AM�ij���ʾ��MC��ƽ�����������ߵ�����г�����t�ķ��̽������t��ֵ��
��1����ͼ2�ã���M���˶��ٶ�Ϊ2cm/s��PQ���˶��ٶ�Ϊ1cm/s��
���ı���PQCM��ƽ���ı��Σ���PM��QC��
��AP��AB��AM��AC��
��AB��AC��
��AP��AM����10��t��2t��
��ã�t��![]() ��
��
�൱t��![]() ʱ���ı���PQCM��ƽ���ı��Σ���ʱ��ͼ2�з�ӳ��һ����ĵ���E��
ʱ���ı���PQCM��ƽ���ı��Σ���ʱ��ͼ2�з�ӳ��һ����ĵ���E��![]() ��
��![]() ��
��
�ʴ�Ϊ��2��![]() ��E��
��E��![]() ��
��![]() ����
����
��2����PQ��AC��
���PBQ�ס�ABC��
���PBQ����������PQ��PB��t��
��![]() ����
����![]()
��ã�BF��![]() t��
t��
��FD��BD��BF��8��![]() t��
t��
�֡�MC��AC��AM��10��2t��
��y��![]() ��PQ+MC��FD��
��PQ+MC��FD��![]() ��t+10��2t����8��
��t+10��2t����8��![]() t����
t����![]() t2��8t+40��
t2��8t+40��
��3���������ijһʱ��t��ʹ��M���߶�PC�Ĵ�ֱƽ�����ϣ���MP��MC��
��M��MH��AB����AB��H����ͼ��ʾ��
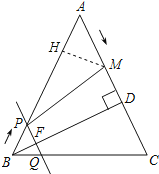
�ߡ�A����A����AHM����ADB��90����
���AHM�ס�ADB��
��![]()
�֡�AD��6��
��![]()
��HM��![]() t��AH��
t��AH��![]() t��
t��
��HP��10��t��![]() t��10��
t��10��![]() t��
t��
��Rt��HMP��MP2����![]() t��2+��10��
t��2+��10��![]() t��2��
t��2��![]() t2��44t+100��
t2��44t+100��
�֡�MC2����10��2t��2��100��40t+4t2��
��MP2��MC2��
��![]() t2��44t+100��100��40t+4t2��
t2��44t+100��100��40t+4t2��
��� t1��![]() ��t2��0����ȥ����
��t2��0����ȥ����
��t��![]() sʱ����M���߶�PC�Ĵ�ֱƽ�����ϣ�
sʱ����M���߶�PC�Ĵ�ֱƽ�����ϣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
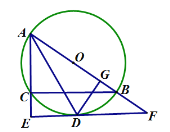
����Ŀ����ͼ����O�ǡ�ABC�����Բ��ABΪ��O��ֱ��������A��ADƽ�֡�BAC����O�ڵ�D������D��BC��ƽ���߷ֱ�AC��AB���ӳ����ڵ�E��F��DG��AB�ڵ�G������BD��
(1)��֤����AED�ס�DGB��
(2)��֤��EF�ǡ�O�����ߣ�
(3)��![]() ��OA��4�����ӻ�
��OA��4�����ӻ�![]() �ij���(���������)��
�ij���(���������)��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪AB��ԲO��ֱ������CD��AB������ΪH����ACƽ�е�ԲO��һ�����߽�CD���ӳ����ڵ�M����AB���ӳ����ڵ�E���е�ΪF������AF��CD�ڵ�N��
��1����֤��CA=CN��
��2������DF����cos��DFA=![]() ��AN=
��AN=![]() ����ԲO��ֱ���ij��ȣ�
����ԲO��ֱ���ij��ȣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ijУ��չ�����������й���Ϊ�������Ӱ������Ҫ�����ѧ��ÿ�˽�һ����Ʒ���ֽ�
������ѡ��50��������Ʒ�ijɼ�����λ������ͳ�����£�
�ȼ� | �ɼ�����m��ʾ�� | Ƶ�� | Ƶ�� |
A | 90�� m ��100 | x | 0.08 |
B | 80�� m ��90 | 34 | y |
C | m ��80 | 12 | 0.24 |
�ϼ� |
| 50 | 1 |
������ϱ��ṩ����Ϣ������������⣺
��1������![]() ��ֵΪ_____________��
��ֵΪ_____________��![]() ��ֵΪ______________����ֱ����д�����
��ֵΪ______________����ֱ����д�����
��2�������β�����Ʒ���A�ȼ���ѧ��������A1��A2��A3������ʾ���ָ�У�����ӱ��β�����Ʒ���A�ȼ���ѧ���У������ȡ����ѧ��̸̸���ǵIJ�����ᣬ��ǡ�ó鵽ѧ��A1��A2�ĸ���Ϊ____________����ֱ����д�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ƽ���ı���ABCD�У�O�ǶԽ���BD���е㣬����O��ֱ��EF�ֱ�DA��BC���ӳ�����E��F��
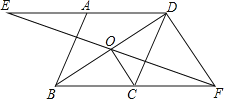
��1����֤��AE��CF��
��2����AE��BC����̽���߶�OC���߶�DF֮��Ĺ�ϵ����˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С����С����Сǿ�����������壬����Լ��������Ӳ��������Ϸ��ʽ��ȷ���ĸ��������壬�������£��������и�����һö�ʵؾ��ȵ�Ӳ�ң�����ͬʱ������Ӳ�����䵽ˮƽ����Ϊһ���غϣ���غ���öӲ���У�ǡ����ö�������ϻ��߷������ϵ����������壻����öӲ�Ҿ�Ϊ�������ϻ������ϣ�����ȷ���������������壮
��1��������������ʾ��Ϸһ���غ����п��ܳ��ֵĽ������״ͼ��
��2�����һ���غ���ȷ����������ĸ��ʣ�
�⣺��1����״ͼΪ��
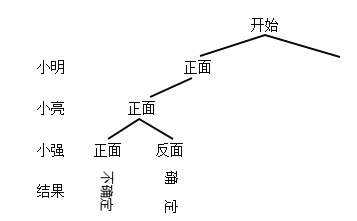
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij���ͺŵ��¿�ˮ��Ĺ��������ǣ���ͨ��Դ���ڳ�ʼ�¶�20���¼���ˮ���е�ˮ����ˮ�´ﵽ�趨�¶�80��ʱ������ֹͣ���˺�ˮ���е�ˮ�¿�ʼ���½������½���20��ʱ���ٴ��Զ�����ˮ���е�ˮ��80��ʱ������ֹͣ����ˮ���е�ˮ���½���20��ʱ���ٴ��Զ����ȣ������������Ϸ�ʽ����ѭ����
С������ѧϰ�����ľ��飬�Ը��ͺ��¿�ˮ���е�ˮ����ʱ��仯�Ĺ��ɽ�����̽��������ˮ��y��ʱ��x�ĺ���������y����λ��������ʾˮ����ˮ���¶ȣ�x����λ��min����ʾ��ͨ��Դ���ʱ�䣮
������С����̽�����̣��벹��������
��1���±���¼��32min��14��ʱ�����¿�ˮ����ˮ���¶�y��ʱ��x�ı仯���
��ͨ��Դ���ʱ��x����λ��min�� | 0 | 1 | 2 | 3 | 4 | 5 | 8 | 10 | 16 | 18 | 20 | 21 | 24 | 32 | �� |
ˮ����ˮ���¶�y����λ������ | 20 | 35 | 50 | 65 | 80 | 64 | 40 | 32 | 20 | m | 80 | 64 | 40 | 20 | �� |
m��ֵΪ ��
��2���ٵ�0��x��4ʱ��д��һ�����ϱ������ݵĺ�������ʽ ��
��4��x��16ʱ��д��һ�����ϱ������ݵĺ�������ʽ ��
����ͼ����ƽ��ֱ������ϵxOy�У�������ϱ��в������ݶ�Ӧ�ĵ㣬��������ĵ㣬������0��x��32ʱ���¶�y��ʱ��x�仯�ĺ���ͼ��
��3�����ˮ��y��ʱ��x�ı仯���ɲ��䣬Ԥ��ˮ�µ�8�δﵽ40��ʱ�������ͨ��Դ min��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��![]() ��
��![]() �ı�
�ı�![]() �Ĵ�ֱƽ���ߣ�����Ϊ��
�Ĵ�ֱƽ���ߣ�����Ϊ��![]() ��
��![]() ��
��![]() ���ӳ��߽��ڵ�
���ӳ��߽��ڵ�![]() ������
������![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ���ڵ�
���ڵ�![]() �������н��ۣ�
�������н��ۣ�
���ı���![]() �����Σ�
������
��![]() ��
��
��![]() ��
��
��![]() �ı���
�ı���![]()
�����ĸ�������������ȷ�Ľ����ǣ� ��

A.�٢�B.�٢ڢ�C.�ڢ�D.�٢ڢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڱ߳�Ϊ1����λ���ȵ�С��������ɵ������У���֪����ı���![]() �������������ߵĽ��㣩���
�������������ߵĽ��㣩���![]() ��
��
��1�����ı���![]() ������ƽ��4����λ���ȣ�������ƽ��6����λ���ȣ��õ��ı���
������ƽ��4����λ���ȣ�������ƽ��6����λ���ȣ��õ��ı���![]() ������ƽ�ƺ���ı���
������ƽ�ƺ���ı���![]() ����
����![]() ,
,![]() ,
,![]() ,
,![]() �Ķ�Ӧ��ֱ�Ϊ��
�Ķ�Ӧ��ֱ�Ϊ��![]() ��
��![]() ��
��![]() ��
��![]() ����
����
��2�����ı���![]() �Ƶ�
�Ƶ�![]() ��ʱ����ת
��ʱ����ת![]() ���õ��ı���
���õ��ı���![]() ��������ת����ı���
��������ת����ı���![]() ����
����![]() ,
,![]() ,
,![]() ,
,![]() �Ķ�Ӧ��ֱ�Ϊ��
�Ķ�Ӧ��ֱ�Ϊ��![]() ��
��![]() ��
��![]() ��
��![]() ����
����
��3����գ���![]() ��
��![]() �ľ���Ϊ________��
�ľ���Ϊ________��
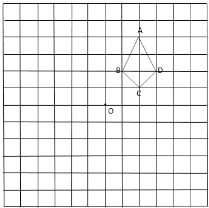
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com