
【题目】阅读下列推理过程,在括号中填写理由. 已知:如图,点D,E分别在线段AB、BC上,AC∥DE,DF∥AE交BC于点F,AE平分∠BAC.求证:DF平分∠BDE
证明:∵AE平分∠BAC(已知)
∴∠1=∠2()
∵AC∥DE(已知)
∴∠1=∠3()
故∠2=∠3()
∵DF∥AE(已知)
∴∠2=∠5()
∴∠3=∠4()
∴DE平分∠BDE()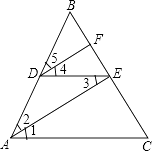
【答案】角平分线的定义;两直线平行,内错角相等;等量代换;两直线平行,同位角相等;等量代换;角平分线的定义
【解析】证明:∵AE平分∠BAC(已知) ∴∠1=∠2(角平分线的定义)
∵AC∥DE(已知)
∴∠1=∠3(两直线平行,内错角相等)
故∠2=∠3(等量代换)
∵DF∥AE(已知)
∴∠2=∠5(两直线平行,同位角相等)
∴∠3=∠4(等量代换)
∴DE平分∠BDE(角平分线的定义).
所以答案是:角平分线的定义,两直线平行,内错角相等,等量代换,两直线平行,同位角相等,等量代换,角平分线的定义.
【考点精析】本题主要考查了平行线的性质的相关知识点,需要掌握两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,∠A=60°,AD=2,AB=3,点M,N分别为线段BC,AB上的动点(含端点,但点M不与点B重合),点E,F分别为DM,MN的中点,则EF长度的最大值为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们把使得函数值为零的自变量的值称为函数的零点. 例如,对于函数y=-x+1,令y=0,可得x=1,我们就说x=1是函数y=-x+1的零点.己知函数y=x2-2(m+1)x-2(m+2)
(m为常数) .(1)当m=-1时,求该函数的零点;
(2)证明:无论m取何值,该函数总有两个零点;
(3)设函数的两个零点分别为![]() 和
和![]() ,且
,且![]() ,求此时的函数解析式,并判断点(n+2,n2-10)是否在此函数的图象上.
,求此时的函数解析式,并判断点(n+2,n2-10)是否在此函数的图象上.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一名射击爱好者7次射击的中靶环数如下(单位:环):7,10,9,8,7,9,9,这7个数据的中位数是( )
A.7环B.8环C.9环D.10环
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△ABC的三个顶点的坐标分别为(-3,2),(-1,3),(2,1).
(1)作出与△ABC关于x轴对称的△A1B1C1(点A,B,C的对应点分别是A1,B1,C1);
(2)连接AA1,CC1,求出四边形AA1 C1C的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线l1∥l2 , 直线l与l1、l2分别交于A、B两点,点M,N分别在l1、l2上,点M,N,P均在l的同侧(点P不在l1、l2上),若∠PAM=α,∠PBN=β. 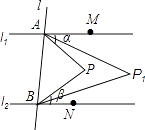
(1)当点P在l1与l2之间时. 求∠APB的大小(用含α、β的代数式表示);
(2)若∠APM的平分线与∠PBN的平分线交于点P1 , ∠P1AM的平分线与∠P1BN的平分线交于点P2 , …,∠Pn﹣1AM的平分线与∠Pn﹣1BN的平分线交于点Pn , 则∠AP1B= , ∠APnB= . (用含α、β的代数式表示,其中n为正整数)
(3)当点P不在l1与l2之间时. 若∠PAM的平分线与∠PBN的平分线交于点P,∠P1AM的平分线与∠P1BN的平分线交于点P2 , …,∠Pn﹣1AM的平分线与∠Pn﹣1BN的平分线交于点Pn , 请直接写出∠APnB的大小.(用含α、β的代数式表示,其中n为正整数)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知,BD为△ABC的角平分线,且BD=BC,E为BD延长线上的一点,BE=BA.下列结论:①△ABD≌△EBC;②AC=2CD;③AD=AE=EC;④∠BCE+∠BCD=180°.其中正确的是
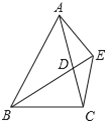
A. ①②③ B. ①②④ C. ①③④ D. ②③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com