
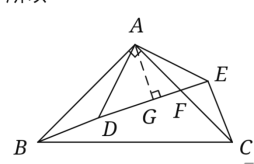
【题目】如图,在△ABC 中,∠BAC=90°,AB=AC=12cm,点 D 为△ABC 内一点,∠BAD=15°,AD= 4 ![]() cm,连接 BD,将△ABD 绕点 A 按逆时针方向旋转,使 AB 与 AC 重合,点 D 的对应点点 E,连接 DE,DE 交 AC 于点 F,则 CF 的长为__________cm.
cm,连接 BD,将△ABD 绕点 A 按逆时针方向旋转,使 AB 与 AC 重合,点 D 的对应点点 E,连接 DE,DE 交 AC 于点 F,则 CF 的长为__________cm.

【答案】4
【解析】
根据旋转的性质以及直角三角形的性质得出△DAE是等腰直角三角形,进而求出DE的长度和叫FAG的度数,再利用直角三角形中30°的性质以及三角函数计算即可得出答案.
如图所示,过点A作BE的垂线交BE于点G
根据旋转的性质可知:AB=AC=12cm
∴AD=AE=![]() cm,∠BAD=∠CAE=15°
cm,∠BAD=∠CAE=15°
∵∠BAC=90°,即∠BAD+∠DAF=90°
∴∠CAE+∠DAF=90°,即∠DAE=90°
∵AD=AE
∴△DAE是等腰直角三角形
∴∠AED=45°,DE=![]() cm
cm
∵AG⊥DE
∴∠EAG=45°
∵∠CAE=15°
∴∠FAG=∠EAG-∠EAF=30°
∵AG=![]() DE=
DE=![]() cm
cm
∴AF= cm
cm
∴CF=AC-AF=12-8=4cm
故答案为4.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】有足够多的长方形和正方形卡片,如下图:

(1)如果选取1号、2号、3号卡片分别为l张、1张、2张,可拼成一个长方形(不重叠无缝隙),请画出这个长方形(所画图形大小和原图保持一致),并用等式表示拼图前后面积之间的关系:
(2)小明用类似方法解释分解因式a2+5ab+4b2,请画图说明小明的方法(所画图形大小和原图保持一致),并写出分解因式的结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB∥CD,∠DCE的角平分线CG的反向延长线和∠ABE的角平分线BF交于点F,∠E﹣∠F=36°,则∠E=( )

A.82°B.84°C.97°D.90°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】三角形ABC(记作△ABC)在8×8方格中,位置如图所示,A(﹣2,1),B(﹣1,4).
(1)请你在方格中建立直角坐标系,并写出C点的坐标;
(2)把△ABC向上平移2个单位长度,再向右平移3个单位长度,请你画出平移后的△A1B1C1,若△ABC内部一点P的坐标为(a,b),则点P的对应点P1的坐标是 .
(3)在x轴上存在一点D,使△DBC的面积等于3,则点D的坐标为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知ADBC,BC,垂足分别为D、F,23180,试说明:GDCB,请补充说明过程,并在括号内填上相应的理由。

解:ADBC,EFBC(已知)
ADBEFB90( ① ),
EF//AD( ② ),
③ 2180( ④ ),
又23180(已知),
13( ⑤ ),
AB// ⑥ ( ⑦ ),
∴∠GDC=∠B( ⑧ )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在正方形![]() 和正方形
和正方形![]() 中,边
中,边![]() 在边
在边![]() 上,
上,![]() 正方形
正方形![]() 绕点
绕点![]() 按逆时针方向旋转
按逆时针方向旋转![]()
(1)如图2,当![]() 时,求证:
时,求证:![]() ;
;
(2)在旋转的过程中,设![]() 的延长线交直线
的延长线交直线![]() 于点
于点![]() .①如果存在某一时刻使得
.①如果存在某一时刻使得![]() ,请求出此时
,请求出此时![]() 的长;②若正方形
的长;②若正方形![]() 绕点
绕点![]() 按逆时针方向旋转了
按逆时针方向旋转了![]() ,求旋转过程中,点
,求旋转过程中,点![]() 运动的路径长.
运动的路径长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司生产一种新型生物医药产品,生产成本为2万元/ 吨,每月生产能力为12吨,且生产出的产品都能销售出去.这种产品部分内销,另一部分外销(出口),内销与外销的单价![]() (单位:万元/吨)与销量的关系分别如图1,图2.
(单位:万元/吨)与销量的关系分别如图1,图2.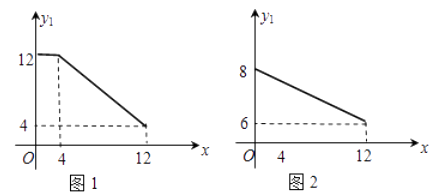
(1)如果该公司内销数量为x(单位:吨),内、外销单价分别为y 1 , y 2 ,求, ![]() 关于x的函数解析式;
关于x的函数解析式;
(2)如果该公司内销数量为x(单位:吨),求内销获得的毛利润 ![]() 关于x的函数解析式;
关于x的函数解析式;
(3)请设计一种销售方案,使该公司本月能获得最大毛利润,并求出毛利润的最大值.(毛利润=销售收入-生产成本).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com