
【题目】如图,学校位于小亮家北偏东35°方向,距离为300m,学校位于大刚家南偏东85°方向,距离也是300m,则大刚家相对于小亮家的位置是_______。

【答案】北偏西25°距离为300m
【解析】
由题意可知,小亮家、大刚家和学校构成了一个等边三角形,再根据“上北下南,左西右东“即可得出刚家相对与小亮家的位置.
解:如图所示:
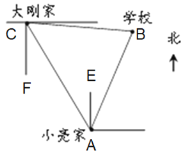
∵学校位于小亮家北偏东35°方向,距离为300m,学校位于大刚家南偏东85°方向,距离也是300m,
∴AB=BC, ∴∠BCA=∠BAC,
设∠CAE=∠FCA=x,
∴∠BCF-∠FCA=∠BAE+∠CAE,即85°-x=35°+x
∴x=25°, ∴∠BCA=60°, ∴△ABC为等边三角形,AB=BC=AC=300m,
∴大刚家相对于小亮家的位置是北偏西25°方向,距离为300m.
故答案为北偏西25°方向,距离为300m.


科目:初中数学 来源: 题型:
【题目】已知二次函数y=-(a+b)x2-2cx+a-b,a、b、c是△ABC的三边
(1) 当抛物线与x轴只有一个交点时,判断△ABC是什么形状
(2) 当![]() 时,该函数有最大值
时,该函数有最大值![]() ,判断△ABC是什么形状
,判断△ABC是什么形状
查看答案和解析>>
科目:初中数学 来源: 题型:
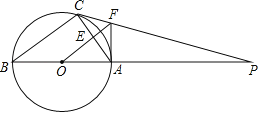
【题目】如图,![]() 内接于
内接于![]() ,AB是直径,
,AB是直径,![]() 的切线PC交BA的延长线于点P,
的切线PC交BA的延长线于点P,![]() 交AC于点E,交PC于点F,连接AF;
交AC于点E,交PC于点F,连接AF;
![]() 判断AF与
判断AF与![]() 的位置关系并说明理由.
的位置关系并说明理由.
![]() 若
若![]() 的半径为8,
的半径为8,![]() ,求AC的长.
,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方形AOCB的顶点A(m,n)和C(p,q)在坐标轴上,已知![]() 和
和![]() 都是方程x+2y=4的整数解,点B在第一象限内.
都是方程x+2y=4的整数解,点B在第一象限内.
(1)求点B的坐标;
(2)若点P从点A出发沿y轴负半轴方向以1个单位每秒的速度运动,同时点Q从点C出发,沿x轴负半轴方向以2个单位每秒的速度运动,问运动到多少秒时,四边形BPOQ面积为长方形ABCO面积的一半;
(3)如图2,将线段AC沿x轴正方向平移得到线段BD,点E(a,b)为线段BD上任意一点,试问a+2b的值是否变化?若变化,求其范围;若不变化,求其值.(直接写出结论)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知⊙O是以AB为直径的△ABC的外接圆,过点A作⊙O的切线交OC的延长线于点D,交BC的延长线于点E.
(1)求证:∠DAC=∠DCE;
(2)若AB=2,sin∠D=![]() ,求AE的长.
,求AE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形OABC摆放在平面直角坐标系![]() 中,点A在
中,点A在![]() 轴上,点C在
轴上,点C在![]() 轴上,OA=8,OC=6.
轴上,OA=8,OC=6.


(1)求直线AC的表达式
(2)若直线![]() 与矩形OABC有公共点,求
与矩形OABC有公共点,求![]() 的取值范围;
的取值范围;
(3)若点O与点B位于直线![]() 两侧,直接写出
两侧,直接写出![]() 的取值范围。
的取值范围。
查看答案和解析>>
科目:初中数学 来源: 题型:
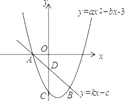
【题目】抛物线y=ax2+bx﹣3(a≠0)与直线y=kx+c(k≠0)相交于A(﹣1,0)、B(2,﹣3)两点,且抛物线与y轴交于点C.
(1)求抛物线的解析式;
(2)求出C、D两点的坐标
(3)在第四象限抛物线上有一点P,若△PCD是以CD为底边的等腰三角形,求出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
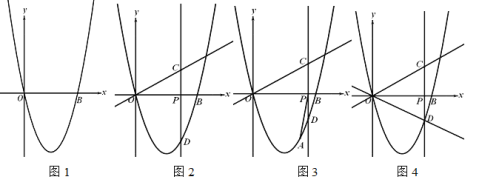
【题目】已知,二次函数![]() 的图像与x轴的一个交点为O(0,0),点P(m,0)是x轴正半轴上的一个动点.
的图像与x轴的一个交点为O(0,0),点P(m,0)是x轴正半轴上的一个动点.
(1)如图1,求二次函数的图像与x轴另一个交点的坐标;
(2)如图2,过点P作x轴的垂线交直线![]() 与点C,交二次函数图像于点D,
与点C,交二次函数图像于点D,
①当PD=2PC时,求m的值;
如图3,已知A(3,-3)在二次函数图像上,连结AP,求![]() 的最小值;
的最小值;
(3如图4,在第(2)小题的基础上,作直线OD,作点C关于直线OD的对称点C’,当C’落在坐标轴上时,请直接写出m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】跳跳一家外出自驾游,出发时油箱里还剩有汽油30升,已知跳跳家的汽车每百千米的平均油耗为12升,设油箱里剩下的油量为y(单位:升),汽车行驶的路程为x(单位:千米).
(1)求y关于x的函数表达式;
(2)若跳跳家的汽车油箱中的油量低于5升时,仪表盘会亮起黄灯警报. 要使邮箱中的存油量不低于5升,跳跳爸爸至多能够行驶多少千米就要进加油站加油?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com