
【题目】如图,四边形ABCD是⊙O的内接四边形,AC为直径,![]() ,DE⊥BC,垂足为E.
,DE⊥BC,垂足为E.
(1)求证:CD平分∠ACE;
(2)判断直线ED与⊙O的位置关系,并说明理由;
(3)若CE=2,AC=8,阴影部分的面积为 .
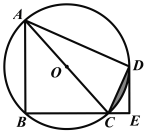
【答案】(1)见解析;(2)直线ED与⊙O相切,见解析;(3)![]()
【解析】
(1)根据圆周角定理,由![]() ,得到∠BAD=∠ACD,再根据圆内接四边形的性质得∠DCE=∠BAD,所以∠ACD=∠DCE,即可证明CD平分∠ACE;
,得到∠BAD=∠ACD,再根据圆内接四边形的性质得∠DCE=∠BAD,所以∠ACD=∠DCE,即可证明CD平分∠ACE;
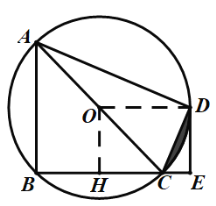
(2)连结OD,如图,利用内错角相等证明OD∥BC,而DE⊥BC,则OD⊥DE,于是根据切线的判定定理可得DE为⊙O的切线;
(3)作OH⊥BC于H,易得四边形ODEH为矩形,所以OD=EH=4,则CH=HECE=2,于是有∠HOC=30°,得到∠COD=60°,然后根据扇形面积公式、等边三角形的面积公式和阴影部分的面积=S扇形OCDS△OCD进行计算即可求得结果.
(1)证明:![]() ,
,
![]() ,
,
∵四边形ABCD内接于⊙O,
∴![]() ,
,
![]() ,
,
![]() ,
,
![]() ,即CD平分∠ACE;
,即CD平分∠ACE;
(2)解:直线ED与⊙O相切,理由如下:
连接OD,
![]() ,
,
![]() ,
,
![]() ,
,
∴OD∥BC,
![]() ,
,
![]() ,
,
![]() 直线ED与⊙O相切;
直线ED与⊙O相切;
(3)解:作OH⊥BC于H,则四边形ODEH为矩形,
∴OD=EH,
∵CE=2,AC=8,
∴OD=OC![]() ,
,
则![]() ,CH=HECE=2,
,CH=HECE=2,
在![]() 中,
中,![]() ,则
,则![]()
∴![]() ,
,
∴阴影部分的面积=S扇形OCDS△OCD
![]()
![]() ,
,
故答案为:![]() .
.


科目:初中数学 来源: 题型:
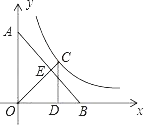
【题目】如图,点A,点B分别在y轴,x轴上,OA=OB,点E为AB的中点,连接OE并延长交反比例函数y=![]() (x>0)的图象于点C,过点C作CD⊥x轴于点D,点D关于直线AB的对称点恰好在反比例函数图象上,则OE﹣EC=_____.
(x>0)的图象于点C,过点C作CD⊥x轴于点D,点D关于直线AB的对称点恰好在反比例函数图象上,则OE﹣EC=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在不透明的袋子中有四张标着数字 ![]() ,
,![]() ,
,![]() ,
,![]() 的卡片,这些卡片除数字外都相同.甲同学按照一定的规则抽出两张卡片,并把卡片上的数字相加.下图是他所画的树状图的一部分.
的卡片,这些卡片除数字外都相同.甲同学按照一定的规则抽出两张卡片,并把卡片上的数字相加.下图是他所画的树状图的一部分.
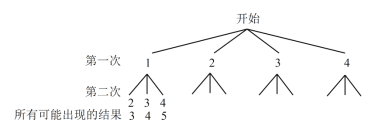
(1)由上图分析,甲同学的游戏规则是:从袋子中随机抽出一张卡片后 (填"放回"或"不放回"),再随机抽出一张卡片;
(2)帮甲同学完成树状图;
(3)求甲同学两次抽到的数字之和为偶数的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABE中,∠B=90°,AB=BE,将△ABE绕点A逆时针旋转45°,得到△AHD,过D作DC⊥BE交BE的延长线于点C,连接BH并延长交DC于点F,连接DE交BF于点O.下列结论:①DE平分∠HDC;②DO=OE;③H是BF的中点;④BC-CF=2CE;⑤CD=HF,其中正确的有( )
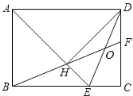
A.5个B.4个C.3个D.2个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,∠ACB=30°,将一块直角三角板的直角顶点P放在两对角线AC,BD的交点处,以点P为旋转中心转动三角板,并保证三角板的两直角边分别于边AB,BC所在的直线相交,交点分别为E,F.
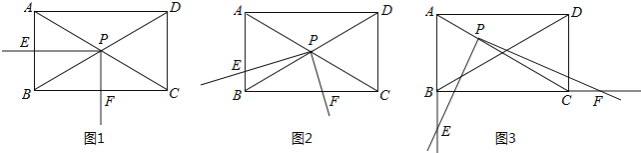
(1)当PE⊥AB,PF⊥BC时,如图1,则![]() 的值为 ;
的值为 ;
(2)现将三角板绕点P逆时针旋转α(0°<α<60°)角,如图2,求![]() 的值;
的值;
(3)在(2)的基础上继续旋转,当60°<α<90°,且使AP:PC=1:2时,如图3,![]() 的值是否变化?证明你的结论.
的值是否变化?证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在我市迎接奥运圣火的活动中,某校教学楼上悬挂着宣传条幅DC,小丽同学在点A处,测得条幅顶端D的仰角为30°,再向条幅方向前进10米后,又在点B处测得条幅顶端D的仰角为45°,已知测点A、B和C离地面高度都为1.44米,求条幅顶端D点距离地面的高度.(计算结果精确到0.1米,参考数据:![]() .)
.)
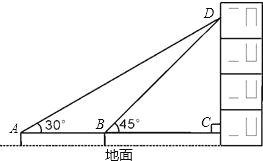
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在锐角三角形ABC中,BC=4,∠ABC=60°,BD平分∠ABC,交AC于点D,M,N分别是BD,BC上的动点,则CM+MN的最小值是( )
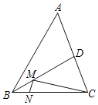
A. ![]() B. 2C. 2
B. 2C. 2![]() D. 4
D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一只不透明的袋子中装有标号分别为1、2、3、4、5的5个小球,这些球除标号外都相同.
(1)从袋中任意摸出一个球,摸到标号为偶数的概率是 ;
(2)先从袋中任意摸出一个球后不放回,将球上的标号作为十位上的数字,再从袋中任意摸出一个球,将球上的标号作为个位上的数字,请用画树状图或列表的方法求组成的两位数是奇数的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com