
【题目】在平面直角坐标系中,A(a,0),B(b,0),C(﹣1,c)(见图1),且 ![]()
![]() .
.

(1)求a、b、c的值;
(2)①在x轴的正半轴上存在一点M,使三角形COM的面积是三角形ABC的面积的一半,求出点M的坐标;
②在坐标轴的其它位置是否存在点M,使三角形COM的面积三角形ABC的面积的一半仍然成立? 若存在,请直接写出符合条件的点M的坐标;
(3)如图2,过点C作CD⊥y轴交y轴于点D,点P为线段CD延长线上的一动点,连接OP,OE平分∠AOP,OF⊥OE.当点P运动时,![]() 的值是否会改变?若不变,求其值;若改变,说明理由.
的值是否会改变?若不变,求其值;若改变,说明理由.
【答案】(1)a=-2,b=3,c=2;(2)①M(![]() ,0)或(-
,0)或(-![]() ,0),②存在,满足条件的点M坐标为(0,5)或(0,-5);(3)结论:
,0),②存在,满足条件的点M坐标为(0,5)或(0,-5);(3)结论:![]() 的值是定值,
的值是定值,![]() =2.
=2.
【解析】
(1)根据绝对值、二次根式和平方的非负性,可得到![]() ,(c-2)2=0,计算即可解得a、b、c的值;
,(c-2)2=0,计算即可解得a、b、c的值;
(2)由(1)可知A(-2,0),B(3,0),分情况讨论:①由题意设点M的坐标为(x,0),在OM=![]() ,结合△COM的面积是△ABC面积的一半,列出方程,解方程结合点M在x轴的正半轴即可求得此时点M的坐标;
,结合△COM的面积是△ABC面积的一半,列出方程,解方程结合点M在x轴的正半轴即可求得此时点M的坐标;
②由①中的结果可得点M在x轴负半轴时的坐标;当M在y轴上时,可设点M的坐标为(0,y),结合△COM的面积是△ABC面积的一半,列出方程,解方程即可求得点M在y轴上的符合条件的坐标;
(3)由题意易证∠AOE+∠FOG=90°,∠FOG=∠POF,∠DOE=∠FOG,由此可得到∠OPD=∠POG=2∠FOG,从而可得![]() =2.
=2.
(1)因为![]()
![]() ,根据绝对值、二次根式和平方的非负性,可以得到
,根据绝对值、二次根式和平方的非负性,可以得到![]() ,(c-2)2=0,解
,(c-2)2=0,解![]() 得到a=-2,b=3;因为(c-2)2=0,所以c=2,故a=-2,b=3,c=2;
得到a=-2,b=3;因为(c-2)2=0,所以c=2,故a=-2,b=3,c=2;
(2)解:由(1)可知A(-2,0),B(3,0),则分情况讨论点M:
①当M在x轴上时,设M(m,0),由题意:![]() |m|2=
|m|2=![]()
![]()
![]()
![]() 5
5![]() ,
,
∴m=±![]() ,
,
∴M(![]() ,0)或(-
,0)或(-![]() ,0).
,0).
②当M在y轴上时,设M(0,m),由题意:![]() |m|1=
|m|1=![]()
![]()
![]()
![]() 5
5![]() 2,
2,
∴m=±5,
∴M(5,0)或(0,-5),
综上所述,满足条件的点M坐标为M(![]() ,0)或(-
,0)或(-![]() ,0)或(0,5)或(0,-5).
,0)或(0,5)或(0,-5).
(3)解:如图中,结论:![]() 的值是定值,
的值是定值,![]() =2.
=2.

理由:∵OE⊥OF,
∴∠EOF=90°,
∴∠AOE+∠FOG=90°,
∵∠AOE=∠EOP,∠EOP+∠POF=90°,
∴∠FOG=∠POF,
∵∠DOE+∠AOE=90°,∠AOE+∠FOG=90°,
∴∠DOE=∠FOG,
∵CP∥AG,
∴∠OPD=∠POG=2∠FOG,
∴∠OPD=2∠FOG,
∴![]() =2.
=2.


科目:初中数学 来源: 题型:
【题目】二次函数 ![]() 的图象与
的图象与 ![]() 轴交于
轴交于 ![]() (1, 0),
(1, 0), ![]() 两点,与
两点,与 ![]() 轴交于点
轴交于点 ![]() ,其顶点
,其顶点 ![]() 的坐标为(-3, 2).
的坐标为(-3, 2).
(1)求这二次函数的关系式;
(2)求 ![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=-x2-2x+3的图象与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,点D为抛物线的顶点.
(1)求点A、B、C的坐标;
(2)点M为线段AB上一点(点M不与点A、B重合),过点M作x轴的垂线,与直线AC交于点E,与抛物线交于点P,过点P作PQ∥AB交抛物线于点Q,过点Q作QN⊥x轴于点N,若点P在点Q左边,当矩形PMNQ的周长最大时,求△AEM的面积;
(3)在(2)的条件下,当矩形PMNQ的周长最大时,连接DQ,过抛物线上一点F作y轴的平行线,与直线AC交于点G(点G在点F的上方).若, ![]() 求点F的坐标.
求点F的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了培养学生的阅读习惯,某校开展了“读好书,助成长”系列活动,并准备购置一批图书,购书前 ,对学生喜欢阅读的图书类型进行了抽样调查,并将调查数据绘制成两幅不完整的统计图,如图所示,根据统计图所提供的信息,回答下列问题: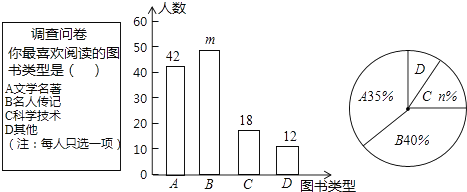
(1)本次调查共抽查了名学生,两幅统计图中的m= , n=.
(2)已知该校共有960名学生,请估计该校喜欢阅读“A”类图书的学生约有多少人?
(3)学校要举办读书知识竞赛,七年(1)班要在班级优胜者2男1女中随机选送2人参赛,求选送的两名参赛学生为1男1女的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知线段![]()

(1)如图1,点![]() 沿线段
沿线段![]() 自点
自点![]() 向点
向点![]() 以
以![]() 的速度运动,同时点
的速度运动,同时点![]() 沿线段点
沿线段点![]() 向点
向点![]() 以
以![]() 的速度运动,几秒钟后,
的速度运动,几秒钟后,![]() 两点相遇?
两点相遇?
(2)如图1,几秒后,点![]() 两点相距
两点相距![]() ?
?
(3)如图2,![]() ,
,![]() ,当点
,当点![]() 在
在![]() 的上方,且
的上方,且![]() 时,点
时,点![]() 绕着点
绕着点![]() 以30度/秒的速度在圆周上逆时针旋转一周停止,同时点
以30度/秒的速度在圆周上逆时针旋转一周停止,同时点![]() 沿直线
沿直线![]() 自
自![]() 点向
点向![]() 点运动,假若点
点运动,假若点![]() 两点能相遇,求点
两点能相遇,求点![]() 的运动速度.
的运动速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=6,BC=4,过对角线BD中点O的直线分别交AB,CD边于点E,F.
(1)求证:四边形BEDF是平行四边形;
(2)当四边形BEDF是菱形时,求EF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点 ![]() 、
、 ![]() 、
、 ![]() 的坐标分别为
的坐标分别为 ![]() 、
、 ![]() 、
、 ![]() ,先将
,先将 ![]() 沿一确定方向平移得到
沿一确定方向平移得到 ![]() ,点
,点 ![]() 的对应点
的对应点 ![]() 的坐标是
的坐标是 ![]() ,再将
,再将 ![]() 绕原点
绕原点 ![]() 顺时针旋转
顺时针旋转 ![]() 得到
得到 ![]() ,点
,点 ![]() 的对应点为点
的对应点为点 ![]() .
.
(1)画出 ![]() 和
和 ![]() ;
;
(2)求出在这两次变换过程中,点 ![]() 经过点
经过点 ![]() 到达
到达 ![]() 的路径总长;
的路径总长;
(3)求线段 ![]() 旋转到
旋转到 ![]() 所扫过的图形的面积.
所扫过的图形的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的布口袋里装有白、红、黑三种颜色的小球,它们除了颜色之外没有其它区别,其中白球2只、红球1只、黑球1只. 袋中的球已经搅匀.
(1)随机地从袋中摸出1只球,则摸出白球的概率是多少?
(2)随机地从袋中摸出1只球,放回搅匀再摸出第二个球.请你用画树状图或列表的方法表示所有等可能的结果,并求两次都摸出白球的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com