
【题目】结合数轴与绝对值的知识回答下列问题:
一般地,数轴上表示数m和数n的两点之间的距离公式为|m﹣n|.
(1)例如:数轴上表示4和1的两点之间的距离为|4﹣1|=
数轴表示5和﹣2的两点之间的距离为|5﹣(﹣2)|=|5+2|=
(2)数轴上表示数a的点与表示﹣4的点之间的距离表示为
数轴上表示数a的点与表示2的点之间的距离表示为
若数轴上a位于﹣4与2之间,则|a+4|+|a﹣2|的值为 ;
(3)当a= 时,|a+5|+|a﹣1|+|a﹣4|的值最小,最小值为 .
【答案】(1)3;7;(2)|a+4|;|a﹣2|;6;(3)1;9.
【解析】
(1)根据绝对值的性质计算即可;
(2)根据距离公式即可表示,然后根据绝对值的性质化简即可;
(3)先画出数轴,然后利用数轴分类讨论,然后求最小值即可.
解:(1)|4﹣1|=3,|5﹣(﹣2)|=|5+2|=7,
故答案为:3;7.
(2)根据数轴上两点的距离公式:数轴上表示数a的点与表示﹣4的点之间的距离为:|a﹣(﹣4)|=|a+4|;
数轴上表示数a的点与表示2的点之间的距离为|a﹣2|;
当a位于﹣4与2之间时,a+4>0,a﹣2<0
∴|a+4|+|a﹣2|= a+4+2﹣a=6
故答案为:|a+4|;|a﹣2|;6.
(3)根据数轴上两点的距离公式可知:|a+5|表示数a的点与表示﹣5的点之间的距离,|a﹣1|表示数a的点与表示1的点之间的距离,|a﹣4|表示数a的点与表示4的点之间的距离
①若a≤﹣5时,由下图可知:|a﹣4|≥|﹣5﹣4|=9
∴|a+5|+|a﹣1|+|a﹣4|>9;
![]()
②若﹣5<a≤4时,由下图可知:|a+5|+|a﹣4|=|﹣5﹣4|=9
∴|a+5|+|a﹣1|+|a﹣4|≥9(当且仅当|a﹣1|=0,即a=1时,取等号);
![]()
③若4<a时,由下图可知:|a+5|≥|﹣5﹣4|=9,
∴|a+5|+|a﹣1|+|a﹣4|>9.
![]()
综上所述:|a+5|+|a﹣1|+|a﹣4|≥9,故|a+5|+|a﹣1|+|a﹣4|的值最小是9,此时a=1.
故答案为:1;9.


 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,直线y=kx+3与
中,直线y=kx+3与![]() 轴、
轴、![]() 轴分别相交于点A、B,并与抛物线
轴分别相交于点A、B,并与抛物线![]() 的对称轴交于点
的对称轴交于点![]() ,抛物线的顶点是点
,抛物线的顶点是点![]() .
.
(1)求k和b的值;
(2)点G是![]() 轴上一点,且以点
轴上一点,且以点![]() 、C、
、C、![]() 为顶点的三角形与△
为顶点的三角形与△![]() 相似,求点G的坐标;
相似,求点G的坐标;
(3)在抛物线上是否存在点E:它关于直线AB的对称点F恰好在y轴上.如果存在,直接写出点E的坐标,如果不存在,试说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一工地计划租用甲、乙两辆车清理淤泥,从运输量来估算,若租两车合运,10天可以完成任务,若甲车的效率是乙车效率的2倍.
(1)甲、乙两车单独完成任务分别需要多少天?
(2)已知两车合运共需租金65000元,甲车每天的租金比乙车每天的租金多1500元.试问:租甲乙车两车、单独租甲车、单独租乙车这三种方案中,哪一种租金最少?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某服装厂生产一种西装和领带,西装每套定价![]() 元,领带每条定价
元,领带每条定价![]() 元,厂方在开展促销活动期间,向客户提供两种优惠方案:
元,厂方在开展促销活动期间,向客户提供两种优惠方案:
①西装和领带都按定价的![]() 付款;②买一套西装送一条领带。
付款;②买一套西装送一条领带。
现某客户要到该服装厂购买西装![]() 套,领带
套,领带![]() 条
条![]() 。
。
(1)若该客户按方案①购买,需付款多少元?(用含![]() 的代数式表示);
的代数式表示);
(2)若该客户按方案②购买,需付款多少元?(用含![]() 的代数式表示);
的代数式表示);
(3)若![]() ,通过计算说明此时按哪种方案购买较为合算?
,通过计算说明此时按哪种方案购买较为合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】山地自行车越来越受到中学生的喜爱,各种品牌相继投放市场,某车行经营的A型车去年销售总额为5万元,今年每辆销售价比去年降低400元,若卖出的数量相同,销售总额将比去年减少20%.
(1)今年A型车每辆售价多少元?(用列方程的方法解答)
(2)该车行计划新进一批A型车和新款B型车共60辆,且B型车的进货数量不超过A型车数量的两倍,应如何进货才能使这批车获利最多?
A,B两种型号车的进货和销售价格如下表:
A型车 | B型车 | |
进货价格(元) | 1100 | 1400 |
销售价格(元) | 今年的销售价格 | 2000 |
查看答案和解析>>
科目:初中数学 来源: 题型:
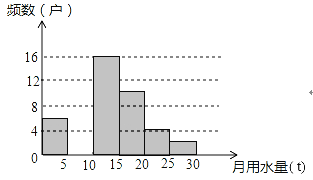
【题目】八年级(1)班同学为了解某小区家庭月均用水情况,随机调査了该小区部分家庭,并将调查数据整理成如下两幅不完整的统计图表:
月均用水量x(t) | 频数(户) | 频率 |
0<x≤5 | 6 | 0.12 |
5<x≤10 | m | 0.24 |
10<x≤15 | 16 | 0.32 |
15<x≤20 | 10 | 0.20 |
20<x≤25 | 4 | n |
25<x≤30 | 2 | 0.04 |
请根据以上信息,解答以下问题:
(1)直接写出频数分布表中的m、n的值并把频数直方图补充完整;
(2)求出该班调查的家庭总户数是多少?
(3)求该小区用水量不超过15的家庭的频率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知MB=ND,∠MBA=∠NDC,下列条件中不能判定△ABM≌△CDN的是( )

A. ∠M=∠N B. AM=CN C. AB=CD D. AM∥CN
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】古希腊著名的毕达哥拉斯学派把1,3,6,10…这样的数称为“三角形数”,而把1,4,9,16…这样的数称为“正方形数”.从图中可以发现,任何一个大于1的“正方形数”都可以看作两个相邻“三角形数”之和.下列等式中,符合这一规律的是( )
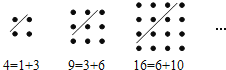
A.13=3+10B.25=9+16C.36=15+21D.49=18+31
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com